Álgebra-Sistema de equações.

por John von Neumann jr Dom 24 Jul 2016, 15:27

Mostre que o sistema [img] Álgebra-Sistema de equações. 1z5nitj

[/img]
não possui soluções reais (x, y, z).

Somando as equações cheguei em:
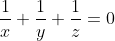$Álgebra-Sistema de equações. Gif$ ,como faço para continuar?

por **Ashitaka** Dom 24 Jul 2016, 20:01

x² - xy + 1 = 0
y² - zy + 1 = 0
z² - xz + 1 = 0

x² + y² + z² - xy - zy - xz + 3 = 0
Multiplicando tudo por 2:
(x² - 2xy + y²) + (x² - 2xz + z²) + (y² - 2yz + z²) + 6 = 0
(x-y)² + (x-z)² + (y-z)² = -6 ----> Não possui soluções reais.