(UEFS) Função
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 (UEFS) Função
(UEFS) Função
Junto a um muro, pretende-se construir um canteiro, conforme a figura, em forma de um triângulo retângulo com catetos de comprimento x e y, em metros, cercando, apenas catetos, com aramado de 20m de comprimento. A área A(x) do canteiro, em função de x, e o valor da maior área que o canteiro pode ter, em metros quadrado, são, respectivamente, iguais a :
A)=(20-x)x)
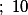
B)=(20-x)x)
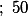
C)=%20-\frac{x^2}{2}%20+%2010x)
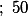
D)=%20\frac{(20-x)x}{2})
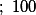
E)=%20(20-x)x)
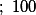

CORRETA: C
A)
B)
C)
D)
E)

CORRETA: C
kauangs- Iniciante
- Mensagens : 47
Data de inscrição : 01/06/2016
Idade : 27
Localização : Bahia
 Re: (UEFS) Função
Re: (UEFS) Função
Achei esta resolução na internet, mas não estou entendendo porque a área máxima corresponde ao Yv da parábola, não consigo enxergar isso na imagem:
Do enunciado tiramos,
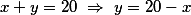
A área do canteiro é a de um triângulo como dito:
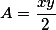
}{2}}) ou
ou 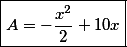
A área máxima corresponde a ordenada do vértice da parábola (ponto máximo da parábola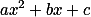 ).
).
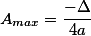
}{4a})
[img]http://www.equacao.mat.br/latex/mathtex.cgi?A_{max}=\frac{-[10^2%20-%20\cancel{4\cdot%20\left(\frac{-1}{2}\right)\cdot%200}]}{4\cdot%20\left(\frac{-1}{2}\right)}[/img]
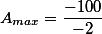
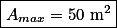
Do enunciado tiramos,
A área do canteiro é a de um triângulo como dito:
A área máxima corresponde a ordenada do vértice da parábola (ponto máximo da parábola
[img]http://www.equacao.mat.br/latex/mathtex.cgi?A_{max}=\frac{-[10^2%20-%20\cancel{4\cdot%20\left(\frac{-1}{2}\right)\cdot%200}]}{4\cdot%20\left(\frac{-1}{2}\right)}[/img]
kauangs- Iniciante
- Mensagens : 47
Data de inscrição : 01/06/2016
Idade : 27
Localização : Bahia
 Re: (UEFS) Função
Re: (UEFS) Função
A parábola representativa da função A = (- 1/2). x² + 10.x tem concavidade voltada para baixo.
O valor máximo da função (a área máxima) ocorre no vértice da parábola.
Abcissa do vértice ---> xV = - b/2a ---> xV = - 10/2.(-1/2) ---> xV = 10
Área máxima ---> Amáx = (-1/2).10² + 10.10 ---> Amáx = 50 m²
O valor máximo da função (a área máxima) ocorre no vértice da parábola.
Abcissa do vértice ---> xV = - b/2a ---> xV = - 10/2.(-1/2) ---> xV = 10
Área máxima ---> Amáx = (-1/2).10² + 10.10 ---> Amáx = 50 m²

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: (UEFS) Função
Re: (UEFS) Função
Ah, sim, muito obrigado!! 
kauangs- Iniciante
- Mensagens : 47
Data de inscrição : 01/06/2016
Idade : 27
Localização : Bahia
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












