Encontre a reta da intersecção dos planos

Escreva as equações paramétricas da reta intersecção dos planos:
alfa: x=-1+h; y=-2; z=-h-u
beta: X=(1,0,3)+h(1,2,0)+u(-1,1,-1)
Muito obrigado.

Para encontrar a reta devemos fazer o produto vetorial entre os vetores diretores normal a cada plano, entretanto, neste caso, devemos primeiramente calcular o vetor normal para depois aplicar o que foi citado. Assim:

 

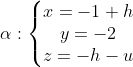
Vetores contidos no plano alfa:
h = (1,0,-1);      u = (0,0,-1);         P(-1,-2,0)

n = h x u --> n = (0,1,0) ---> alfa: y + d = 0

Substituindo P em alfa, vem
alfa: y + 2 = 0            (1)

Agora o mesmo processo para o plano beta. Veja:
h = (1,2,0);           u(-1,1,-1);         P1(1,0,3)

n1 = h x u --> n1 = (-2,3,1) ---> beta: -2x + 3y + z + d = 0
Substituindo P1 em beta, temos:
beta: 2x - 3y - z + 1 = 0     (2)

Agora, devemos encontrar um ponto em comum (interseção) entre os planos, para isso devemos fazer "x=0" nos dois planos.
alfa: y + 2 = 0
beta: -3y - z + 1 = 0

y = -2;      z = 7; ---> I(0,-2,7)

Bom, já temos o ponto em que a reta passa e os vetores para fazer o produtor vetorial. Posso deixar o resto com você?

Um abraço, Lauro.