Polinômio 01

Determine um polinômio p(x) de menor grau possível, com coeficientes inteiros, tal que


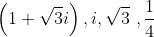
sejam raízes de p(x).

Raízes complexas ou irracionais vem em dupla:

x1 = 1 + i*V3 ----> x2 = 1 - V3 ----> [x - (1 + i*V3)]*[x - (1 - iV3)] = x² - 2x + 4

x3 = i ----> x4 = - i ----> (x - i)*(x + i) = x² +1

x5 = +V3 ----> x6 = -V3 ----> (x - V3)*(x + V3) = x² - 3

x7 = 1/4

P(x) = [(x - x1)*(x - x2)]*[(x - x3)*(x - x4)]*´[(x - x5)*(x - x6)]*(x - x7)

P(x) = (x² - 2x + 4)*(x² + 1)*(x² - 3)*(x - 1/4)

Para se ter todos os coeficientes inteiros basta multiplicar por 4:

P(x) = 4*(x² - 2x + 4)*(x² + 1)*(x² - 3)*(4x - 1)

Bsata agora efetuar as multiplicações para se obter P(x) do 7º grau


Deixo as contas para você fazer.