Questão trigonométrica

por TheUltimateCross Qua 06 Abr 2016, 12:54

Boas pessoal! Alguém me pode explicar como resolver esta questão?

1. Seja f a função definida por:

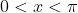$Questão trigonométrica Gif$

Determina

$Questão trigonométrica Gif$

sabendo que

$Questão trigonométrica Gif$

e que $Questão trigonométrica Gif$ .

Obrigado!!

por **Elcioschin** Qua 06 Abr 2016, 13:15

f(x) = 1 + tg[x - pi/3]

f(x - 2.pi/3) = - 2

1 + tg[(x - 2.pi/3) - pi/3] = - 2

tg(x - pi) = - 3

(tgx - tgpi)/(1 + tgx.tgpi) = - 3 ---> (tgx - 0)/(1 + tgx.0) = - 3 ---> tgx = - 3

x está no 2º quadrante ---> senx > 0 e cosx < 0

tgx = - 3 ---> senx/cosx = - 3 ---> sen²x/cos²x = 9 ---> sen²x/(1 - cos²x) = 9 --->

sen²x = 9 - 9.sen²x ---> 10.sen²x = 9 ---> senx = 3√10/10

cos²x = 1 - sen²x ---> cos²x = 1 - 9/10 ---> cos²x = 1/10 ---> cosx = - √10/10

sen(3.pi/2 + x) = sen(3.pi/2).cosx + cos(3.pi/2).senx --->

sen(3.pi/2 + x) = (-1).(-√10/10) + 0.(3.√10/10) ---> sen(3.pi/2 + x) = √10/10