Triângulos quaisquer

por BRUNO BRITO Sáb 12 Mar 2016, 15:16

Um quadrilátero ABCD tem a forma de um losango com ângulos que medem 30°. Se o perímetro desse losango é 8 a sua diagonal maior mede:

Gabarito:

$Triângulos quaisquer Gif$

por **ivomilton** Sáb 12 Mar 2016, 16:03

BRUNO BRITO escreveu:Um quadrilátero ABCD tem a forma de um losango com ângulos que medem 30°. Se o perímetro desse losango é 8 a sua diagonal maior mede:

Gabarito:

$Triângulos quaisquer Gif$

Boa tarde, Bruno.

Se cada ângulo agudo do losango mede 30°, então cada ângulo obtuso deve medir:
(360° - 2*30°)/2 = (360° - 60°)/2 = 300°/2 = 150° cada um.

Aplicando-se a Lei dos Cossenos em relação aos lados que o formam, a fim de determinar a medida do lado oposto, o qual corresponde à diagonal maior do losango:

a² = b² + c² + 2.b.c.cos α

D² = 2² + 2² – 2.2.2.cos.150°
D² = 4 + 4 - 8.(- √3/2)
D² = 8 + 4√3
D² = 4(2 + √3)
D = √[4(2+√3)]
D = 2√(2+√3)

Um abraço.

por BRUNO BRITO Sáb 12 Mar 2016, 16:06

Muitíssimo obrigado! estava tendo dificuldade no final da operação agora entendi. Smile

por **Medeiros** Sáb 12 Mar 2016, 17:33

Eu tinha feito e quando fui salvar desisti porque havia a resposta do Ivomilton -- completa, irretocável.

Mas há a vantagem de se ir acostumando com o valor do cos15°. Por tabela, o sen75°; e, trocando o sinal, também o cos75° e sen15°. E isto, às vezes, facilita nossa vida.

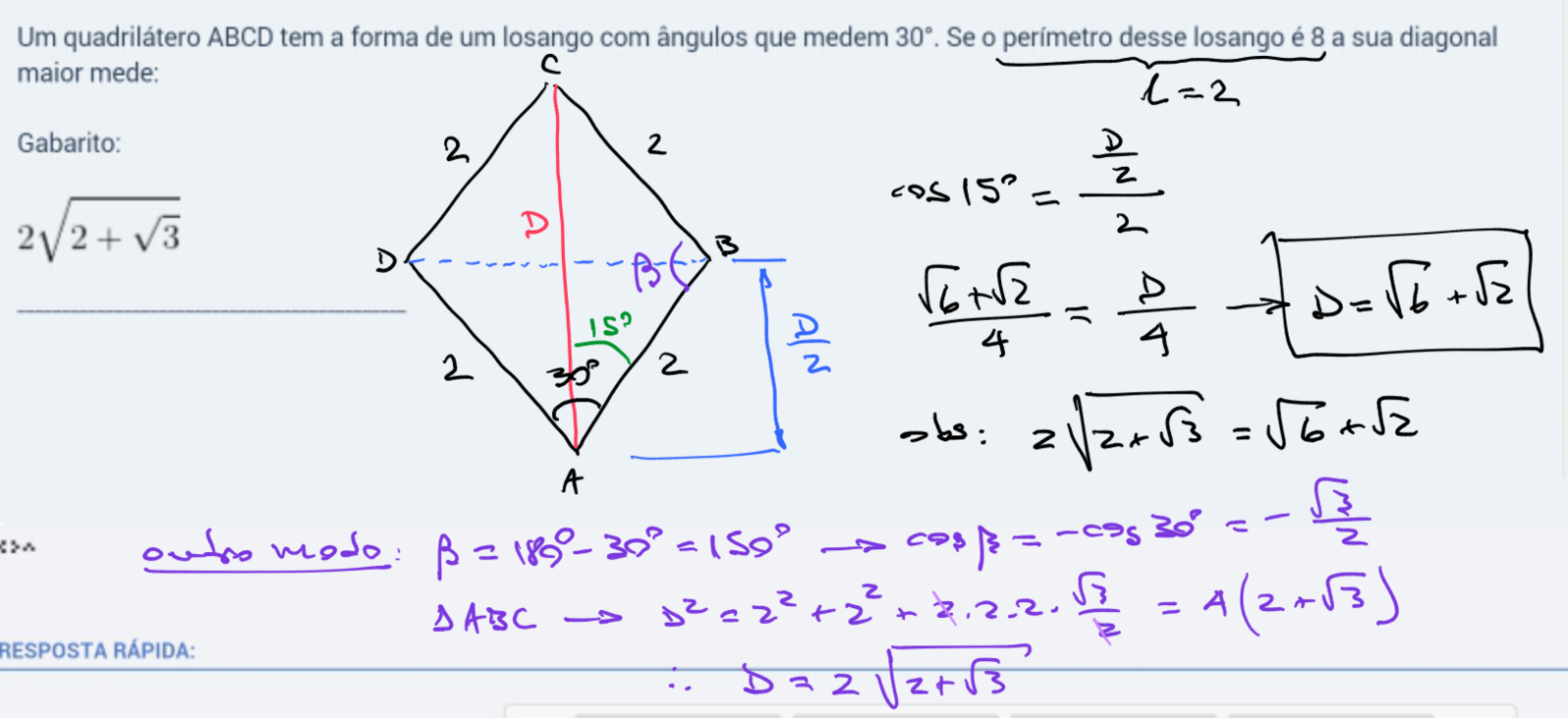
Triângulos quaisquer Eqxz6q