Logaritmo Iezzi B.145
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Logaritmo Iezzi B.145
Logaritmo Iezzi B.145
Se 0 < x ≠ 1, demonstre que:
1/log x (2) * log x (4) + 1/log x (4) * log x (8 ) + ... + 1/ log x (2)^ n -1 * log x (2) ^n = (1 - 1/n) * 1/ log^2 x (2)
Sugestão (do Livro): 1/n (n-1) = 1/n-1 - 1/n
(Sendo que: log x (2), significa log de 2 na base x).
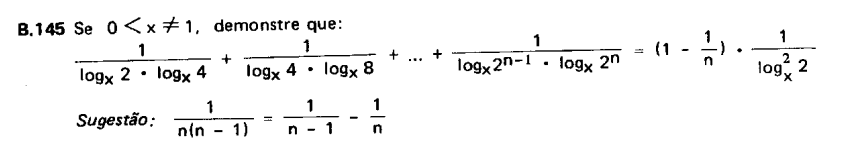
Obrigada.
1/log x (2) * log x (4) + 1/log x (4) * log x (8 ) + ... + 1/ log x (2)^ n -1 * log x (2) ^n = (1 - 1/n) * 1/ log^2 x (2)
Sugestão (do Livro): 1/n (n-1) = 1/n-1 - 1/n
(Sendo que: log x (2), significa log de 2 na base x).
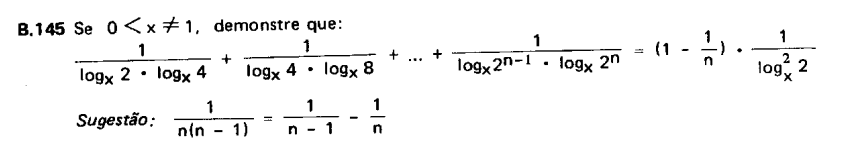
Obrigada.
zirkid- Iniciante
- Mensagens : 5
Data de inscrição : 05/02/2013
Idade : 28
Localização : São Paulo, SP, Brasil
Rei do gagá gosta desta mensagem
 Re: Logaritmo Iezzi B.145
Re: Logaritmo Iezzi B.145
Da sugestão, temos que:
1/( (log[x]2)log[x]4) ) = (1/(log[x]4 - log[x]2) ) ( (1/log[x]2) - (1/log[x]4) )
1/( (log[x]2)log[x]4) ) = (1/log[x]2)( (1/log[x]2) - (1/log[x]4) )
analogamente:
1/( (log[x]4)log[x]8)) = (1/log[x]2)( (1/log[x]4) - (1/log[x]8))
...
1/( (log[x]2^n-1)log[x]2^n) ) = (1/log[x]2)( (1/log[x]2^n-1) - (1/log[x]2^n) )
----------------------> (+) soma telescópica:
S = (1/log[x]2) ( (1/log[x]2) - (1/log[x]2^n) )
S = (1/log[x]2) ( (1/log[x]2) - (1/log[x]2)(1/n) )
S= (1/log²[x]2) ( 1 - (1/n) )
1/( (log[x]2)log[x]4) ) = (1/(log[x]4 - log[x]2) ) ( (1/log[x]2) - (1/log[x]4) )
1/( (log[x]2)log[x]4) ) = (1/log[x]2)( (1/log[x]2) - (1/log[x]4) )
analogamente:
1/( (log[x]4)log[x]8)) = (1/log[x]2)( (1/log[x]4) - (1/log[x]8))
...
1/( (log[x]2^n-1)log[x]2^n) ) = (1/log[x]2)( (1/log[x]2^n-1) - (1/log[x]2^n) )
----------------------> (+) soma telescópica:
S = (1/log[x]2) ( (1/log[x]2) - (1/log[x]2^n) )
S = (1/log[x]2) ( (1/log[x]2) - (1/log[x]2)(1/n) )
S= (1/log²[x]2) ( 1 - (1/n) )

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 31
Localização : RJ
 Re: Logaritmo Iezzi B.145
Re: Logaritmo Iezzi B.145
Obrigada pela ajuda! 
zirkid- Iniciante
- Mensagens : 5
Data de inscrição : 05/02/2013
Idade : 28
Localização : São Paulo, SP, Brasil
 Re: Logaritmo Iezzi B.145
Re: Logaritmo Iezzi B.145
Substituir as incógnitas por indução vulgar é válido?
Apla2004- Iniciante
- Mensagens : 41
Data de inscrição : 02/06/2020
 Re: Logaritmo Iezzi B.145
Re: Logaritmo Iezzi B.145
Não. Quando você substitui a incógnita por um número irá provar a propriedade exclusivamente para aquele número. Porém o enunciado quer uma prova para todos os valores positivos e diferentes de 1.
Rory Gilmore- Monitor

- Mensagens : 1860
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
 Re: Logaritmo Iezzi B.145
Re: Logaritmo Iezzi B.145
Mas no caso N seria igual a isso:
1/( (log[x]2)log[x]4) ) = ( (1/log[x]2) - (1/log[x]4) )
1/( (log[x]2)log[x]4) ) = ( (1/log[x]2) - (1/log[x]4) )
Apla2004- Iniciante
- Mensagens : 41
Data de inscrição : 02/06/2020
 Tópicos semelhantes
Tópicos semelhantes» Logaritmo Iezzi B.144
» Logaritmo - Iezzi
» Logaritmo - (Iezzi) 272
» Logaritmo - (Iezzi)
» Logaritmo IEZZI
» Logaritmo - Iezzi
» Logaritmo - (Iezzi) 272
» Logaritmo - (Iezzi)
» Logaritmo IEZZI
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|













