Números Primos?
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Números Primos?
por daaark14 Sex 19 Jun 2015, 13:52
Os algorismos a, b e c são tais que os números de dois algarismos aa, bc e cb são números primos e aa+bc+cb=aa². Se b < c, então bc é igual a?
R:37
Como resolve esse problema?
R:37
Como resolve esse problema?
Última edição por daaark14 em Sex 19 Jun 2015, 14:07, editado 1 vez(es)
daaark14- Iniciante
- Mensagens : 25
Data de inscrição : 18/04/2015
Idade : 28
Localização : Alagoas
Re: Números Primos?
por Smasher Sex 19 Jun 2015, 14:06
Parece ter faltado uma parte da questão, por favor verifique.
Smasher- Mestre Jedi
- Mensagens : 583
Data de inscrição : 20/03/2015
Idade : 28
Localização : São Paulo, SP, Brasil
daaark14- Iniciante
- Mensagens : 25
Data de inscrição : 18/04/2015
Idade : 28
Localização : Alagoas
Re: Números Primos?
por Smasher Sex 19 Jun 2015, 14:31
1) aa é um número primo de dois algarismos iguais que só pode ser 11, já que todos os outros de dois algarismo iguais são múltiplos de 11, ou seja, não são primos.
2) Todo número (na base 10) com n algarismos do tipo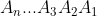
pode ser escrito desta maneira :
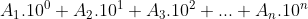
Basicamente, vamos poder escrever bc e cb assim:
bc = 10b+c
cb = 10c+b
3) Então temos:
aa+bc+cb=(aa)²
11 + (10b + c) + (10c + b) = 121
11b + 11c = 110
11(b+c) = 110
b+c = 10
Os dois números cuja soma é igual a dez, em que possam ser algarismos de dois números primos é
3 e 7. Como b< c, b =3 e c=7 e bc = 37
2) Todo número (na base 10) com n algarismos do tipo
Basicamente, vamos poder escrever bc e cb assim:
bc = 10b+c
cb = 10c+b
3) Então temos:
aa+bc+cb=(aa)²
11 + (10b + c) + (10c + b) = 121
11b + 11c = 110
11(b+c) = 110
b+c = 10
Os dois números cuja soma é igual a dez, em que possam ser algarismos de dois números primos é
3 e 7. Como b< c, b =3 e c=7 e bc = 37
Smasher- Mestre Jedi
- Mensagens : 583
Data de inscrição : 20/03/2015
Idade : 28
Localização : São Paulo, SP, Brasil
Tópicos semelhantes» Qual a proporção entre números primos e não primos?
» Números Prímos
» Números primos
» Numeros Primos
» Números primos
» Números Prímos
» Números primos
» Numeros Primos
» Números primos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
