Na figura abaixo, ABCD é um quadrado de lado
5 participantes
Página 1 de 1
Na figura abaixo, ABCD é um quadrado de lado
por OliviaTate Qua 22 Abr 2015, 17:48
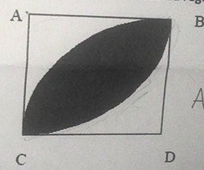
Na figura abaixo, ABCD é um quadrado de lado 8 cm. Os arcos que limitam a zona preta tem raios iguais a 8 cm, e seus respectivos centros em A e D. Determine a área da região escura.
Gabarito 36,6
Gabarito 36,6
OliviaTate- Mestre Jedi
- Mensagens : 635
Data de inscrição : 27/01/2014
Idade : 27
Localização : São Paulo, SP, Brasil
Re: Na figura abaixo, ABCD é um quadrado de lado
por Carlos Adir Qua 22 Abr 2015, 17:55
1°) Calcule a área do quadrado, chamemos de Q
2°) Calcule a área do setor circular ABC, chamemos de area M
3°) Subtraia a area do setor restante, isto é, Q-M.
4°) Multiplicamos por 2 para saber a área branca total, o resultado é 2(Q-M)
5°) Peque a área do quadrado e subtraia a área branca. Isto é, Q-2(Q-M)=2M-Q
Assim, temos:
&space;-&space;l^2&space;\\&space;Area&space;=&space;r^2&space;\left(\dfrac{\pi-2}{2}&space;\right&space;) "\\ Area = 2 \left(\dfrac{\pi r^2}{4} \right ) - l^2 \\ Area = r^2 \left(\dfrac{\pi-2}{2} \right )")
Usando o raio = 8, e pi =3,14, obtemos:
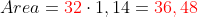
Corrigido
2°) Calcule a área do setor circular ABC, chamemos de area M
3°) Subtraia a area do setor restante, isto é, Q-M.
4°) Multiplicamos por 2 para saber a área branca total, o resultado é 2(Q-M)
5°) Peque a área do quadrado e subtraia a área branca. Isto é, Q-2(Q-M)=2M-Q
Assim, temos:
Usando o raio = 8, e pi =3,14, obtemos:
Corrigido
Última edição por Carlos Adir em Qua 22 Abr 2015, 19:22, editado 1 vez(es) (Motivo da edição : Correção)
____________________________________________
← → ↛ 
⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
Re: Na figura abaixo, ABCD é um quadrado de lado
por CaiqueF Qua 22 Abr 2015, 18:01
Imagina a circunferência completa de centro D e raio 8.
A sua área será 64pi, que dividindo por 4 fica 16pi.
O que resultaria na área pintada mais a area de um dos lados brancos.
Agora voce subtrai a area do triangulo BCD, que é 8*8/2 = 32
Ficando 16pi-32. O que resulta em metade da área sombreada. Então basta multiplicarmos por 2.
(16pi-32)2 = 32pi-64
Se não entender avisa que eu tento fazer um desenho.
A sua área será 64pi, que dividindo por 4 fica 16pi.
O que resultaria na área pintada mais a area de um dos lados brancos.
Agora voce subtrai a area do triangulo BCD, que é 8*8/2 = 32
Ficando 16pi-32. O que resulta em metade da área sombreada. Então basta multiplicarmos por 2.
(16pi-32)2 = 32pi-64
Se não entender avisa que eu tento fazer um desenho.
CaiqueF- Monitor
- Mensagens : 1237
Data de inscrição : 16/05/2012
Idade : 28
Localização : Salvador -> São Carlos
Re: Na figura abaixo, ABCD é um quadrado de lado
por Elcioschin Qua 22 Abr 2015, 18:09
Outro modo
Trace a diagonal BC, dividindo a "pétala negra" em duas áreas iguais a s. A área procurada vale 2.s
s = área do quadrante de círculo - área do triângulo retângulo isósceles de lado L = 8
s = pi.R²/4 - L²/8 ---> s = pi.8²/4 - 8²/2 ---> s = 16.pi - 32 ---> s = 16.(pi - 2)
2s = 32.(pi - 2) ~= 36,5
Carlos digitou errado 36, quando deveria ser 32
Trace a diagonal BC, dividindo a "pétala negra" em duas áreas iguais a s. A área procurada vale 2.s
s = área do quadrante de círculo - área do triângulo retângulo isósceles de lado L = 8
s = pi.R²/4 - L²/8 ---> s = pi.8²/4 - 8²/2 ---> s = 16.pi - 32 ---> s = 16.(pi - 2)
2s = 32.(pi - 2) ~= 36,5
Carlos digitou errado 36, quando deveria ser 32
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Na figura abaixo, ABCD é um quadrado de lado
por OliviaTate Qua 22 Abr 2015, 18:24
Perfeito, obrigada mestres
OliviaTate- Mestre Jedi
- Mensagens : 635
Data de inscrição : 27/01/2014
Idade : 27
Localização : São Paulo, SP, Brasil
Re: Na figura abaixo, ABCD é um quadrado de lado
por Medeiros Qui 23 Abr 2015, 03:00
Outro modo.
A1 = área do setor circular = 16.pi
A2 = área do quadrado = 64
A = 2×A1 - A2
note que os dois setores circulares se sobrepõe na pétala, logo a pétala foi contada duas vezes. Ao subtrair o quadrado, tiramos uma vez a pétala e toda a área branca que foi contada uma vez em cada setor circular.
A = 32.pi - 64 = 32 (pi -2)
A1 = área do setor circular = 16.pi
A2 = área do quadrado = 64
A = 2×A1 - A2
note que os dois setores circulares se sobrepõe na pétala, logo a pétala foi contada duas vezes. Ao subtrair o quadrado, tiramos uma vez a pétala e toda a área branca que foi contada uma vez em cada setor circular.
A = 32.pi - 64 = 32 (pi -2)
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» (UFPE) Na figura abaixo o retângulo ABCD de l
» Área - Na figura abaixo ABCD é um quadrado de
» Área - Na figura abaixo ABCD é um quadrado de
» A figura representa um quadrado ABCD de lado
» Na figura abaixo, ABCD é um retângulo.
» Área - Na figura abaixo ABCD é um quadrado de
» Área - Na figura abaixo ABCD é um quadrado de
» A figura representa um quadrado ABCD de lado
» Na figura abaixo, ABCD é um retângulo.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
