Círculos interseccionados
4 participantes
Página 1 de 1
 Círculos interseccionados
Círculos interseccionados
(UFRGS 2013) Observe a figura abaixo:

No quadrado ABCD de lado 2, os lados AB e BC são diâmetros dos semicírculos. A área da região sombreada é
a) 3 – π/4
b) 4 – π/2
c) 3 - π
d) 4 - π
e) 3 – π/2
Por favor, poderiam me explicar como se consegue a área dos círculos interseccionados?
Obrigado

No quadrado ABCD de lado 2, os lados AB e BC são diâmetros dos semicírculos. A área da região sombreada é
a) 3 – π/4
b) 4 – π/2
c) 3 - π
d) 4 - π
e) 3 – π/2
Por favor, poderiam me explicar como se consegue a área dos círculos interseccionados?
Obrigado
Mathematicien- Mestre Jedi

- Mensagens : 668
Data de inscrição : 14/08/2014
 Re: Círculos interseccionados
Re: Círculos interseccionados
Modifique o olhar sobre a figura

a área não hachurada tem o tamanho de
- um semi-círculo de raio 1
- um quadrado de lado 1

a área não hachurada tem o tamanho de
- um semi-círculo de raio 1
- um quadrado de lado 1
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Círculos interseccionados
Re: Círculos interseccionados
Boa tarde,Mathematicien escreveu:(UFRGS 2013) Observe a figura abaixo:
No quadrado ABCD de lado 2, os lados AB e BC são diâmetros dos semicírculos. A área da região sombreada é
a) 3 – π/4
b) 4 – π/2
c) 3 - π
d) 4 - π
e) 3 – π/2
Por favor, poderiam me explicar como se consegue a área dos círculos interseccionados?
Obrigado
A área comum aos dois semicírculos é igual a:
[S(círculo) - S(quadrado inscrito)]/4 * 2 = [S(círculo) - S(quadrado inscrito)]/2
S(círculo) = πr² = π(2/2)² = π
S(quadrado inscrito) = (2/√2)² = (2√2/2)² = (√2)² = 2
Área comum aos dois semicírculos = (π - 2)/2
Área da região sombreada = S(quadrado) - S(círculo) + área comum =
= 2² - π + (π - 2)/2 = 4 - π + (π - 2)/2 = (8 - 2π + π - 2)/2 = (6 - π)/2 = 3 - π/2
Alternativa (E)
Explicando:
A extensão da parte comum aos dois semicírculos é igual ao lado do quadrado inscrito no círculo (completo).
Um abraço.

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 Re: Círculos interseccionados
Re: Círculos interseccionados
ivomilton escreveu:A área comum aos dois semicírculos é igual a:
[S(círculo) - S(quadrado inscrito)]/4 * 2 = [S(círculo) - S(quadrado inscrito)]/2
Não entendi muito bem a que quadrado o senhor se refere. Se o senhor se refere à figura do Euclides, então por que a área comum aos dois semicírculos é igual a (1/4 da área do círculo - 1/4 da área do quadrado) * 2 ? Por favor, poderia esmiuçar um pouquinho mais?
Obrigado
Mathematicien- Mestre Jedi

- Mensagens : 668
Data de inscrição : 14/08/2014
 Re: Círculos interseccionados
Re: Círculos interseccionados
Boa tarde,Mathematicien escreveu:ivomilton escreveu:A área comum aos dois semicírculos é igual a:
[S(círculo) - S(quadrado inscrito)]/4 * 2 = [S(círculo) - S(quadrado inscrito)]/2
Não entendi muito bem a que quadrado o senhor se refere. Se o senhor se refere à figura do Euclides, então por que a área comum aos dois semicírculos é igual a (1/4 da área do círculo - 1/4 da área do quadrado) * 2 ? Por favor, poderia esmiuçar um pouquinho mais?
Obrigado
Vou tentar esclarecer:
Aquela parte comum aos dois semicírculos (semelhante a uma bola de rugbi), conforme abaixo:
https://www.google.com.br/?gfe_rd=cr&ei=acGiVKupAYaj8wfB1YHoDg&gws_rd=ssl#q=imagem+de+uma+bola+de+rugby
Essa parte podemos dividi-la ao meio, em seu sentido longitudinal, através de um segmento de reta.
Tal segmento de reta é igual à medida de um quadrado que poderá ser inscrito em um círculo de raio igual à metade do lado do quadrado ABCD, ou seja:
raio = 2 cm/2 = 1 cm.
Então, o que percebi foi o seguinte:
A medida da área sombreada é igual à:
Área do quadrado ABCD menos a soma da área dos dois semicírculos (=área do círculo completo), mais a área comum (em forma de uma bola de rugby).
Para calcular essa área comum aos dois semicírculos, pensei assim:
Da área de um círculo completo (=referida soma dos dois semicírculos), subtrair a área do quadrado nele inscrito, cujo lado é igual à medida longitudinal da referida parte comum em formato de bola de rugby.
A área restante será formada por quatro segmentos circulares (ao redor do quadrado inscrito), medindo cada um exatamente a metade da área em forma da referida 'bola'.
Como a parte comum entre os 2 semicírculos contém medida igual a dois desses segmentos circulares, fica: Área comum = (área do círculo – área do quadrado inscrito)/4 x 2.
Espero que você consiga entender estas explicações...
Um abraço.

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 Re: Círculos interseccionados
Re: Círculos interseccionados
Mathematicien escreveu:Por favor, poderiam me explicar como se consegue a área dos círculos interseccionados?
Obrigado
Mathematicien,
acho que o Euclides já lhe deu a melhor resposta para este problema. Entretanto, considerando apenas sua pergunta final, apresento minha contribuição para o esclarecimento.
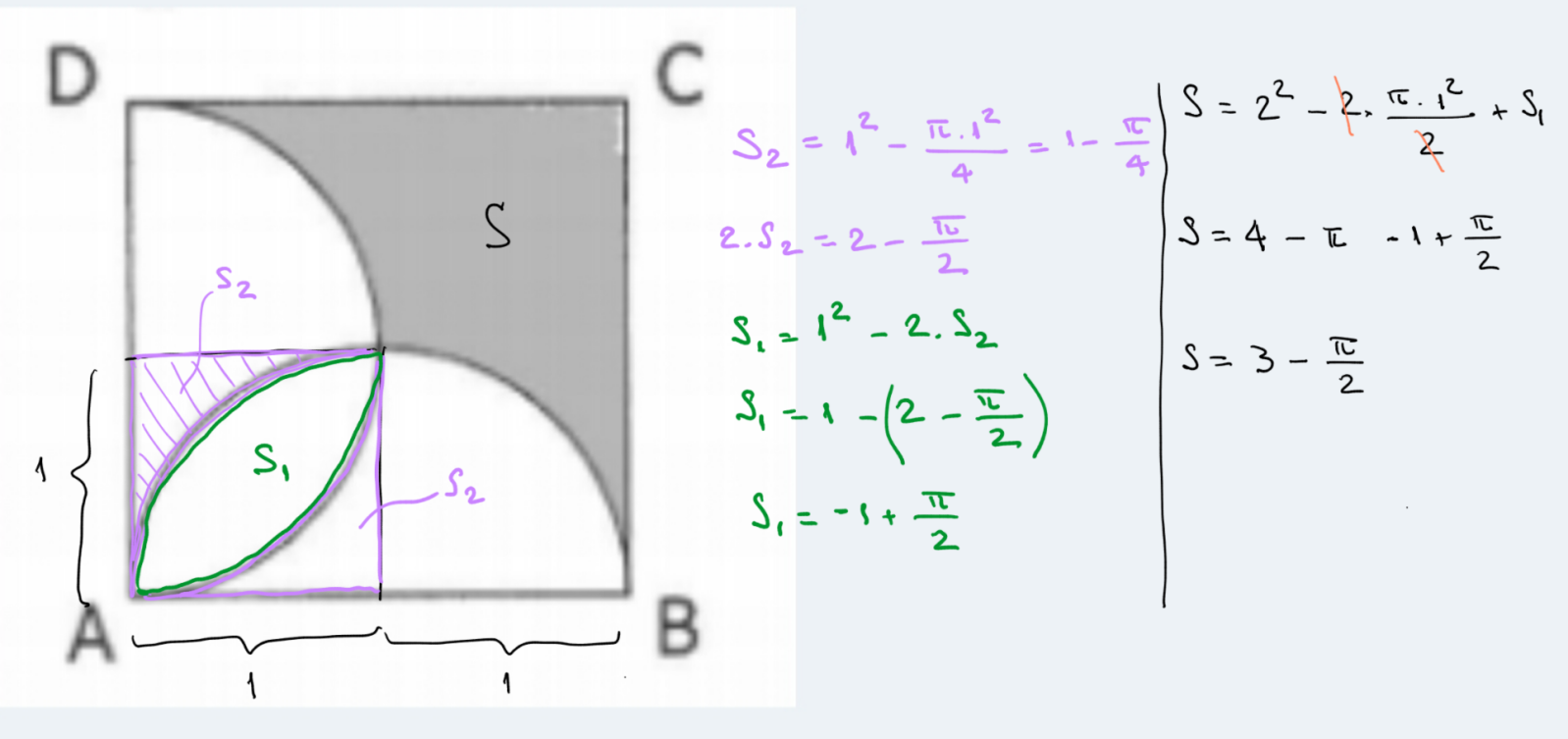

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Círculos interseccionados
Re: Círculos interseccionados
Obrigado a todos vocês pelas ótimas respostas e pela ajuda!
Mathematicien- Mestre Jedi

- Mensagens : 668
Data de inscrição : 14/08/2014
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












