Círculos
3 participantes
Página 1 de 1
Círculos
por alansilva Seg 06 Jan 2014, 16:44
Os círculos de centros O1 e O2 são tangentes entre si no ponto T, e à Reta R, nos pontos Q e R, respectivamente, conforme a figura.
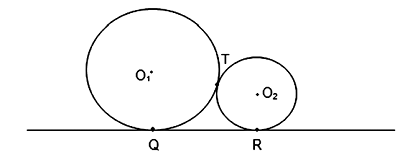
Se QR= 17 cm e QT= 15 cm, então:
A) RT=20 cm
B) RT=12 cm
C) RT=8 cm
D) RT=10 cm
Se QR= 17 cm e QT= 15 cm, então:
A) RT=20 cm
B) RT=12 cm
C) RT=8 cm
D) RT=10 cm
- Gabarito C:
- Gabarito C
____________________________________________
No meio da dificuldade se encontra a oportunidade (Albert Einstein)
alansilva- Elite Jedi
- Mensagens : 958
Data de inscrição : 27/07/2013
Idade : 40
Localização : Rio de Janeiro
Re: Círculos
por Medeiros Seg 06 Jan 2014, 17:55
Gosto de trabalhar com uma letra só. Então, seja:
x = RT o segmento desejado;
a, b, c, m, n = os ângulos assinalados no desenho.
Considere o trapézio QO1O2R. Os ângulos a e b são suplementares: -----> a + b = 180º .........(I)
Considere o triângulo isósceles O1QT.
2m = 180º - a ------> a = 180º - 2m ............(II)
Considere o triângulo isósceles O2RT.
2n = 180º - b ------> b = 180º - 2n ..............(III)
fazendo (II)+(III) e já substituindo (I), vem:
180º = 360º - (2m+2n)
∴ m+n = 90º
Como os raio que ligam estão O1O2 alinhados (ângulo raso), concluímos que o ângulo c é reto.
Logo, c=90º e o triângulo QRT é retângulo em T.
Podemos usar o teorema de Pitágoras.
x² = 17² - 15² ------> x=8
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Círculos
por ivomilton Seg 06 Jan 2014, 18:12
Boa noite, Alan.alansilva escreveu:Os círculos de centros O1 e O2 são tangentes entre si no ponto T, e à Reta R, nos pontos Q e R, respectivamente, conforme a figura.
Se QR= 17 cm e QT= 15 cm, então:
A) RT=20 cm
B) RT=12 cm
C) RT=8 cm
D) RT=10 cm
- Gabarito C:
Ligue seguintes pontos:
O1O2, O2R, RQ e QO1.
A seguir, baixe uma perpendicular desde T até a reta suporte de QR, identificando sua interseção com ela com a letra M.
Ligue também:
QT e RT.
Note então que o triângulo QTR é retângulo em T.
Prova:
^QO1T + ^RO2T = 180° (são suplementares).
^TQM (ângulo de segmento) = 1/2 do ^QO1T.
^TRM (tb ângulo de segmento) = 1/2 do ^RO2T.
Portanto,
^TQM + TRM = 1/2 de 180° = 90°
Sendo assim, o ^QTR é igual a 180° - 90° = 90°, ou seja, triângulo QTR é retângulo!
Portanto, aplicando-se Pitágoras, fica:
(QT)² + (RT)² = (QR)²
15² + (RT)² = 17²
(RT)² = 289 - 225 = 64
RT = √64
RT = 8 cm
Alternativa (C)
ivomilton- Membro de Honra
- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
Re: Círculos
por alansilva Seg 06 Jan 2014, 18:27
Obrigado a todos
____________________________________________
No meio da dificuldade se encontra a oportunidade (Albert Einstein)
alansilva- Elite Jedi
- Mensagens : 958
Data de inscrição : 27/07/2013
Idade : 40
Localização : Rio de Janeiro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
