Numeros Complexos
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Numeros Complexos
Numeros Complexos
Não sei se é a área correta. Caso seja, movam o tópico, por favor.
Sejam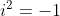 ,
,  um numero complexo,
um numero complexo, 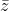 o seu conjugado e
o seu conjugado e  o seu módulo. Julgue os itens a seguir:
o seu módulo. Julgue os itens a seguir:
[...] b) Se é tal que
é tal que  , então
, então  .
.
__________________
>> Além disso, posso fatorar números complexos desta forma z² + z = z(z + 1) ? E sendo w = -1 um número complexo, w^6 é necessariamente = 1 ?
Sejam
[...] b) Se
__________________
>> Além disso, posso fatorar números complexos desta forma z² + z = z(z + 1) ? E sendo w = -1 um número complexo, w^6 é necessariamente = 1 ?
Última edição por PedroBR em Seg 28 Jul 2014, 22:03, editado 1 vez(es)
PedroBR- Iniciante
- Mensagens : 21
Data de inscrição : 04/03/2014
Idade : 44
Localização : Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
Olá, PedroBR.
Primeira dúvida:
Note que z^0 + z^1 + z^2 + z^3 + z^4 + z^5 - creio que você digitou errado - é uma soma de P.G. de a1 = 1, q= z, n = 6 . Assim:
S = 0 \therefore \frac{a_1 \cdot (q^n - 1)}{q - 1} = 0 \therefore \frac{1 \cdot (z^6-1)}{z-1} = 0 \therefore \Leftrightarrow z^6 = 1
Logo, a afirmativa é falsa.
Segunda dúvida:
Sim.
Terceira dúvida:
Sim, pois -1 elevado a expoente par é sempre 1.
Att.,
Pedro
Primeira dúvida:
Note que
Logo, a afirmativa é falsa.
Segunda dúvida:
Sim.
Terceira dúvida:
Sim, pois -1 elevado a expoente par é sempre 1.
Att.,
Pedro

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
PedroBR
1) Seu enunciado está incompleto: Poste TODOS os ítens!!!
2) Não entendi o item b) e z ≠ 1 .... ---> Parece estra incompleto
3) "E sendo w = - 1 um número complexo ...." ---> -1 é um número REAL
1) Seu enunciado está incompleto: Poste TODOS os ítens!!!
2) Não entendi o item b) e z ≠ 1 .... ---> Parece estra incompleto
3) "E sendo w = - 1 um número complexo ...." ---> -1 é um número REAL

Elcioschin- Grande Mestre

- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Numeros Complexos
Re: Numeros Complexos
Élcio, o conjunto dos complexos engloba o dos reais. Todo número real é complexo.
w = - 1 .:. w = -1 + 0i
w = - 1 .:. w = -1 + 0i

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
Desculpa, mas acabei postando a equação errada mesmo. A correta seria:PedroCunha escreveu:Olá, PedroBR.
Primeira dúvida:
Note quez^0 + z^1 + z^2 + z^3 + z^4 + z^5 - creio que você digitou errado - é uma soma de P.G. dea1 = 1, q= z, n = 6 . Assim:S = 0 \therefore \frac{a_1 \cdot (q^n - 1)}{q - 1} = 0 \therefore \frac{1 \cdot (z^6-1)}{z-1} = 0 \therefore \Leftrightarrow z^6 = 1
Logo, a afirmativa é falsa.
Segunda dúvida:
Sim.
Terceira dúvida:
Sim, pois -1 elevado a expoente par é sempre 1.
Att.,
Pedro
PedroBR- Iniciante
- Mensagens : 21
Data de inscrição : 04/03/2014
Idade : 44
Localização : Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
Muda tudo.
z + z^2 + z^3 + z^4 + z^5 = 0 \therefore \frac{z \cdot (z^5 - 1)}{z-1} = 0 \therefore z \cdot (z^5 - 1) = 0
Se z^5 = 1 , z^5 -1 = 0 e com isso z \cdot (z^5-1) = 0 \therefore 0 = 0
Verdadeira.
Se
Verdadeira.

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
O gabarito diz que ela é falsa. Outra coisa: lá em cima você disse que z^6 = 1 era falso por quê ?
PedroBR- Iniciante
- Mensagens : 21
Data de inscrição : 04/03/2014
Idade : 44
Localização : Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
Porque era z^6 = 1 e não z^5 = 1 .
Tem certeza do enunciado?
Do jeito que você passou na sua 2ª mensagem, a afirmativa é verdadeira.
Tem certeza do enunciado?
Do jeito que você passou na sua 2ª mensagem, a afirmativa é verdadeira.

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
Não consegui achar a resolução da questão na internet, mas o que você mostrou já me ajudou muito. Valeu !
Agora, outra duvida: Sendo o numero complexo z = i + 1 uma das raízes do polinômio x³-4x²+6x-4, é correto afirmar que a soma das outras raízes é um numero complexo de módulo, igual a ...
Consegui resolver a questão, mas quero saber se há outro modo mais simples de fazer isto. Resolva, por favor.
Agora, outra duvida: Sendo o numero complexo z = i + 1 uma das raízes do polinômio x³-4x²+6x-4, é correto afirmar que a soma das outras raízes é um numero complexo de módulo, igual a ...
Consegui resolver a questão, mas quero saber se há outro modo mais simples de fazer isto. Resolva, por favor.
PedroBR- Iniciante
- Mensagens : 21
Data de inscrição : 04/03/2014
Idade : 44
Localização : Brasil
 Re: Numeros Complexos
Re: Numeros Complexos
Apenas uma questão por tópico. Crie um novo tópico para essa nova questão.

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Números complexos
» FPP - Números Complexos
» Números Complexos
» Números complexos
» Números complexos
» FPP - Números Complexos
» Números Complexos
» Números complexos
» Números complexos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












