Vetores?

por playstadion Ter 24 Jun 2014, 19:20

Considere W o subespaço de R ^4 gerado pelos elementos v1=( 1, -1, 0, 0), v2=(0,0,1,1,), v3=(-2, 2, 1, 1) e v4=( 1, 0, 0, 0).

a) Mostre que u= (2, -3, 2, 2) pertence W.

b) Exiba uma base para W e determine a sua dimensão.

c) Mostre que W diferente de R^4.

por Matheus Fillipe Qua 25 Jun 2014, 13:22

Olá Playstation, Se W é grado pelos vetores dados temos que um vetor V pertencente a W é dado por:

$V=av_1+bv_2+cv_3+dv_4$

Assim o sistema equivalente, sendo e f g h as componentes de V:

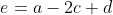
$e=a-2c+d$

$f=-a+2c$

$g=b+c$

$h=b+c$

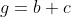
Veja que g=h para qualquer a, b, c ou d. O que isso significa? Que W é o conjunto dos vetores da forma:

$V=(e,f,g,g)$

Já que o sistema terá solução para qualquer e ,f e g, a restrição está na última equação. Com isso esse é um sistema possível indeterminado. Em outras palavras W é o conjunto dos vetores em R4 com a restrição de que suas duas últimas componentes sejam iguais. Por isso W é diferente de R4. (1,2,3,4) está contido em R4 mas não em W. (1,2,3,3) está em w. C respondida.

A a já está respondida, qualquer vetor em R4 que tenha duas componentes finais iguais está em W. Basta provar que existem a,b,c,d que resolvam o sistema:

$2=a-2c+d$

$-3=-a+2c$

$2=b+c$

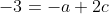
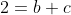
Para responder B, devemos escolher uma base que tenha as duas componentes finais iguais. Poderia ser:

$v_1=(1,0,0,0)\;\;\;v_2=(0,1,0,0)\;\;\;\;v_3(0,0,1,1)\;\;\;v_4=(0,0,1,1)$

Ou simplesmente:

$v_1=(1,0,0,0)\;\;\;v_2=(0,1,0,0)\;\;\;\;v_3(0,0,1,1)$

O que é ideal. Não precisamos de quatro vetores não é? Isso significa que W está em R3. Lembre-se, em R3 se você fixa x=y, por exemplo, tem um plano. Uma superfície em R2. Agora temos uma "superfície" em R3. Mas se quer uma base unitária divida v3 por seu módulo:

$v_1=(1,0,0,0)\;\;\;v_2=(0,1,0,0)\;\;\;\;v_3(0,0,\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$

Vetores?

Vetores?

Re: Vetores?

Um fórum livre e democrático.