questão sobre reta numérica

por Convidado Sex 09 maio 2014, 14:50

Na reta real a seguir, os pontos A, B, C, D e E representam alguns valores de uma variável x. Só dois deles satisfazem a inequação 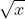$questão sobre reta numérica Gif$ > x. São eles:

questão sobre reta numérica Xopg1w

a) A e B
b) B e C
c) C e D
d) D e E
e) A e D

Como a raiz quadrada de um número pode ser maior que o próprio número? Essa questão é de um simulado para o enem do cursinho da poli e infelizmente não encontrei o gabarito.

por jarry15 Sex 09 maio 2014, 15:15

Olá, Fábio. A raiz quadrada de √x, x ∈ ]0,1[, sempre será maior que o próprio x, logo √x>x apenas para B e C está correto.

Se estiver errado alguem corrija pf..

por Andrew Wiles Sex 09 maio 2014, 15:45

Sim está correto. Um exemplo √0,25=0,5. Sabemos que 0,5 é maior que 0,25.

por Convidado Dom 11 maio 2014, 02:04

obrigado pela explicação nunca iria notar esse ponto da questão sem uma ajuda

por **Elcioschin** Dom 11 maio 2014, 08:46

E esta propriedade pode ser provada:

√x > x ---> elevando ao quadrado:

x > x² ----> x² - x < 0

A função do 1º membro é uma parábola com a concavidade voltada para cima e com raízes x = 0 e x = 1.

Esta função é negativa entre as raízes ----> 0 < x < 1