(Vunesp-SP) Ache os coeficientes angulares
4 participantes
Página 1 de 1
 (Vunesp-SP) Ache os coeficientes angulares
(Vunesp-SP) Ache os coeficientes angulares
(Vunesp-SP) Ache os coeficientes angulares das retas r e s da figura e verifique se elas são perpendiculares.
mr = 2/5, ms = -8/3. Não são perpendiculares.
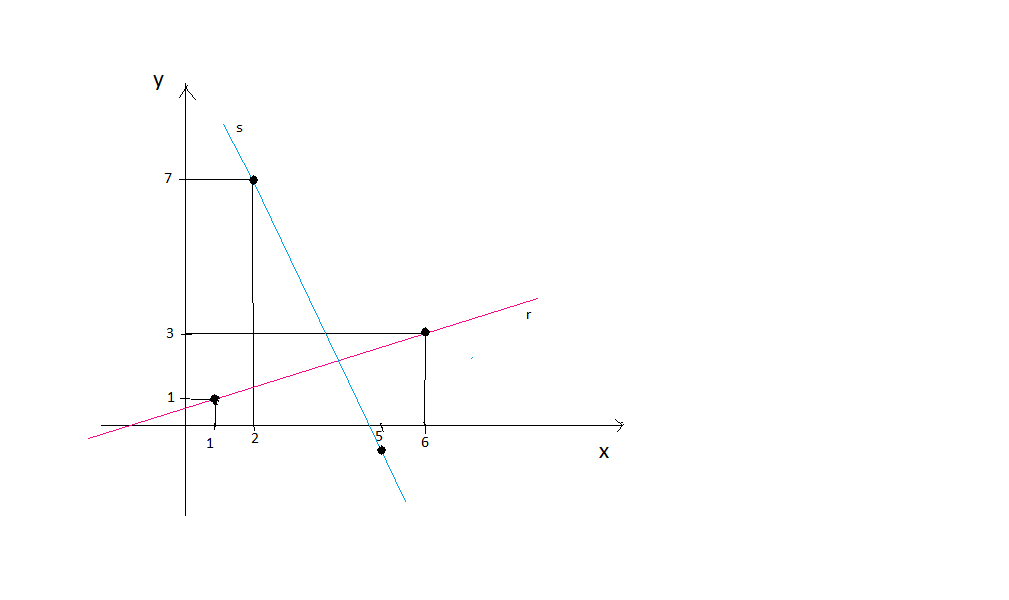
mr = 2/5, ms = -8/3. Não são perpendiculares.
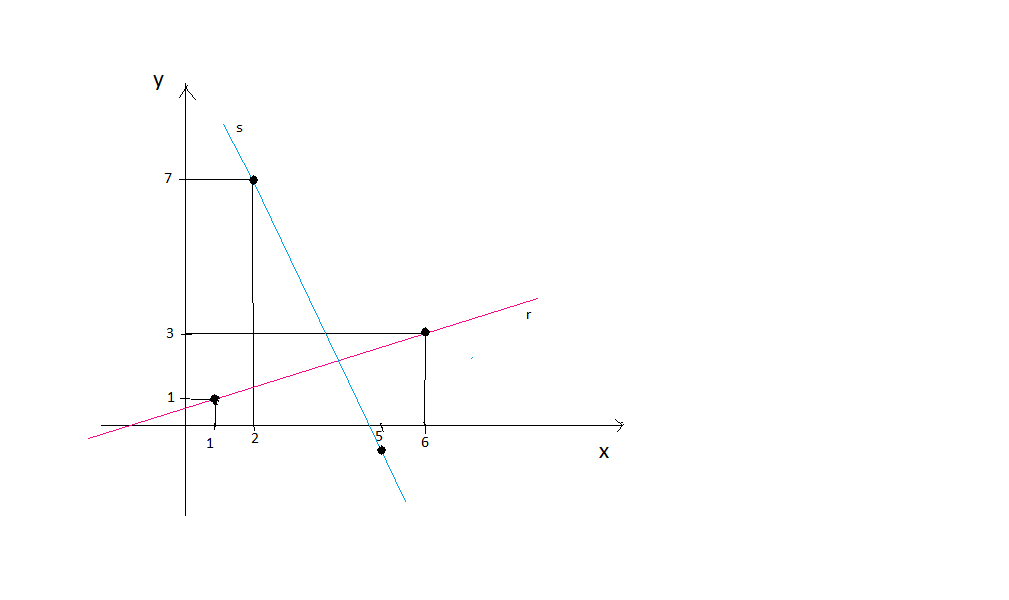

GLAYDSON- Mestre Jedi

- Mensagens : 719
Data de inscrição : 14/11/2012
Idade : 33
Localização : PAULISTA, PERNAMBUCO, BRASIL
 Re: (Vunesp-SP) Ache os coeficientes angulares
Re: (Vunesp-SP) Ache os coeficientes angulares
mr = ∆y / ∆x = 2 / 5
ms = ∆y / ∆x = -8/3
Detalhes:
Na reta r, tome o ponto 1,1 como referencia, e a partir dele você faz as subtrações. ∆y = 3 - 1 e ∆x = 6 - 1
na reta s a mesma coisa, porém ela está inclinada mais de 90 graus, logo o sinal é negativo, e no eixo Y da figura o ponto -1 não está demonstrado.
ms = ∆y / ∆x = -8/3
Detalhes:
Na reta r, tome o ponto 1,1 como referencia, e a partir dele você faz as subtrações. ∆y = 3 - 1 e ∆x = 6 - 1
na reta s a mesma coisa, porém ela está inclinada mais de 90 graus, logo o sinal é negativo, e no eixo Y da figura o ponto -1 não está demonstrado.

raymg3c- Padawan

- Mensagens : 60
Data de inscrição : 23/03/2014
Idade : 28
Localização : Tres coracoes, minas gerais , brasil
 Re: (Vunesp-SP) Ache os coeficientes angulares
Re: (Vunesp-SP) Ache os coeficientes angulares
Oi pessoal, então essa reta seria ortogonal? Bjs
virginiaantunes- Iniciante
- Mensagens : 1
Data de inscrição : 04/04/2015
Idade : 32
Localização : Moc
 Re: (Vunesp-SP) Ache os coeficientes angulares
Re: (Vunesp-SP) Ache os coeficientes angulares
- reta que passa pelos pontos (1, 1 ) e 6, 3 ):
(y-1)/3-1) = ( x-1)/(6-1) -> y = ( 2/5 )*x + ( 3/5 ) -> (r)
- seja a reta perpendicular a (r) que passa pelo ponto ( 2, 7 ):
m = - 5/2
y - 7 = ( - 5/2 )*( x - 2 ) -> y = ( - 5/2 )*x + 12
sabemos que a reta (s) passa pelo ponto ( 5, y ), assim:
x = 5 -> y = ( - 5/2 )*5 + 12 -> y = 1/2 -> ( 5, 1/2 )
assim:
se a ordenada do ponto que faltou apresentar for igual a ( - 1/2 ) as retas serão perpendiculares e caso contrário
serão concorrentes.
* obs: se duas retas estão contidas no plano coordenado elas só poderão ser concorrentes ou paralelas.
(y-1)/3-1) = ( x-1)/(6-1) -> y = ( 2/5 )*x + ( 3/5 ) -> (r)
- seja a reta perpendicular a (r) que passa pelo ponto ( 2, 7 ):
m = - 5/2
y - 7 = ( - 5/2 )*( x - 2 ) -> y = ( - 5/2 )*x + 12
sabemos que a reta (s) passa pelo ponto ( 5, y ), assim:
x = 5 -> y = ( - 5/2 )*5 + 12 -> y = 1/2 -> ( 5, 1/2 )
assim:
se a ordenada do ponto que faltou apresentar for igual a ( - 1/2 ) as retas serão perpendiculares e caso contrário
serão concorrentes.
* obs: se duas retas estão contidas no plano coordenado elas só poderão ser concorrentes ou paralelas.
____________________________________________
...se acupuntura adiantasse, porco-espinho viveria para sempre....

Jose Carlos- Grande Mestre

- Mensagens : 5551
Data de inscrição : 08/07/2009
Idade : 74
Localização : Niterói - RJ
 Tópicos semelhantes
Tópicos semelhantes» coeficientes angulares da tangente e normal
» Possíveis coeficientes angulares de uma reta.
» Aspectos Angulares
» desvios angulares
» Aspectos Angulares
» Possíveis coeficientes angulares de uma reta.
» Aspectos Angulares
» desvios angulares
» Aspectos Angulares
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












