MODULAR
PiR2 :: Matemática :: Álgebra
Página 1 de 1
MODULAR
por biianeves112 Dom 20 Abr 2014, 21:52
Do conjunto solução da inequação é
I X+1 I - I X I (menor é igual a) X+2
I X+1 I - I X I (menor é igual a) X+2
biianeves112- Padawan
- Mensagens : 97
Data de inscrição : 12/02/2013
Idade : 28
Localização : RJ RJ Brail
Re: MODULAR
por Convidado Dom 20 Abr 2014, 23:03
Olá, colega do Fórum Pir2.
Seja a inequação:
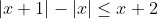
Antes de mais nada temos que:
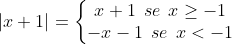
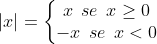
1°) Fazer o quadro de sinais
2°) Através do quadro de sinais, foram geradas três novas inequações, mas sem módulos.
I) - x - 3 ≤ 0 II) x - 1 ≤ 0 III) - x - 1 ≤ 0
x1 ≥ - 3 x2 ≤ 1 x3 ≥ - 1
3°) Fazer a intersecção:
x1 ≥ - 3 e x < - 1 => S1 = {x ∈ ℝ| -3 ≤ x < -1}
x2 ≤ 1 e - 1 ≤ x < 0 => S2 = {x ∈ ℝ| - 1 ≤ x < 0}
x3 ≥ - 1 e x ≥ 0 => S3 = {x ∈ ℝ| x ≥ 0}
4°) A solução do problema é a união entre S1, S2, e S3:
S = {x ∈ ℝ| x ≥ - 3} ou S = [-3; +∞[
Espero tê-la ajudado!
Seja a inequação:
Antes de mais nada temos que:
1°) Fazer o quadro de sinais
2°) Através do quadro de sinais, foram geradas três novas inequações, mas sem módulos.
I) - x - 3 ≤ 0 II) x - 1 ≤ 0 III) - x - 1 ≤ 0
x1 ≥ - 3 x2 ≤ 1 x3 ≥ - 1
3°) Fazer a intersecção:
x1 ≥ - 3 e x < - 1 => S1 = {x ∈ ℝ| -3 ≤ x < -1}
x2 ≤ 1 e - 1 ≤ x < 0 => S2 = {x ∈ ℝ| - 1 ≤ x < 0}
x3 ≥ - 1 e x ≥ 0 => S3 = {x ∈ ℝ| x ≥ 0}
4°) A solução do problema é a união entre S1, S2, e S3:
S = {x ∈ ℝ| x ≥ - 3} ou S = [-3; +∞[
Espero tê-la ajudado!
Última edição por leonardo235 em Dom 20 Abr 2014, 23:22, editado 4 vez(es)
Convidado- Convidado
Re: MODULAR
por Convidado Dom 20 Abr 2014, 23:05
Será que você poderia postar a resposta da questão? Só para confirmar se o cálculo está correto?
Convidado- Convidado
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
