Segundo Grau - IME
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Segundo Grau - IME
por nekobaka Dom 23 Mar 2014, 03:16
Não faço ideia do gabarito. Se ajudar essa prova é de 1999/2000 do IME, A condição que ele comenta que as raízes satisfazem é que a < x1 < b < x2 < c e onde faltam dados é "... tais que a < b < c "
nekobaka- Iniciante
- Mensagens : 12
Data de inscrição : 15/03/2012
Idade : 29
Localização : SSA, BA, BR
Re: Segundo Grau - IME
por PedroCunha Dom 23 Mar 2014, 08:48
Questão já existente no Fórum:
https://pir2.forumeiros.com/t31499-ime-2000-prove-que-a-equacao-possui-exatamente-duas-raizes-reais
https://pir2.forumeiros.com/t31499-ime-2000-prove-que-a-equacao-possui-exatamente-duas-raizes-reais
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
Re: Segundo Grau - IME
por Dela Corte Dom 23 Mar 2014, 09:10
PS: Malditos moderadores, estragando meu trabalho tão suado! Hahahahahaha
Desenvolvendo a equação dada, temos que
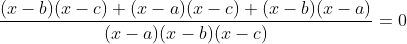
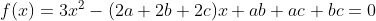
A função f(x) é uma parábola com concavidade voltada para cima. Disso temos que
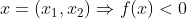
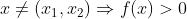
Partindo da consideração inicial, temos a < b < c. Podemos escrever que
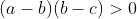
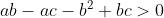
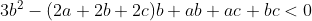
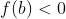
Disso chegamos em (I)
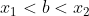
ATENÇÃO: Parece complicado, mas fiz essa parte de trás para frente, considerando primeiro f(b) < 0 e chegando ao fato de que a < b < c. Porém a ordem correta que deve ser apresentada na
resolução da questão é partir de a < b < c e terminar em f(b) < 0.
Por similar raciocínio,
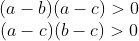
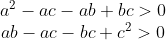
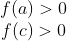
Disso temos (II)
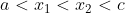
Unindo (I) e (II), temos
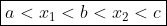
Assim como queríamos provar.
Desenvolvendo a equação dada, temos que
A função f(x) é uma parábola com concavidade voltada para cima. Disso temos que
Partindo da consideração inicial, temos a < b < c. Podemos escrever que
Disso chegamos em (I)
ATENÇÃO: Parece complicado, mas fiz essa parte de trás para frente, considerando primeiro f(b) < 0 e chegando ao fato de que a < b < c. Porém a ordem correta que deve ser apresentada na
resolução da questão é partir de a < b < c e terminar em f(b) < 0.
Por similar raciocínio,
Disso temos (II)
Unindo (I) e (II), temos
Assim como queríamos provar.
Dela Corte- Recebeu o sabre de luz
- Mensagens : 197
Data de inscrição : 31/05/2013
Idade : 27
Localização : Jacareí, São Paulo
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
Tópicos semelhantes» funcao do primeiro grau e segundo grau
» Segundo Grau I
» F. Segundo Grau
» Segundo Grau II
» Segundo Grau III
» Segundo Grau I
» F. Segundo Grau
» Segundo Grau II
» Segundo Grau III
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
