Inequação logarítmica

por davidjordao Ter 18 Mar 2014, 15:31

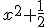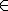Seja f(x) o logaritmo de 2x na base $Inequação logarítmica Mimetex$ .

Resolva a inequação f(x) > 1.

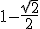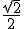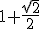Segundo o site onde achei a questão, a resposta é v= {x $Inequação logarítmica Mimetex$ R | 0 < x < $Inequação logarítmica Mimetex$ ou $Inequação logarítmica Mimetex$ < x < $Inequação logarítmica Mimetex$ }

Obrigado desde já.

por Luck Ter 18 Mar 2014, 16:27

log[x²+(1/2)] 2x > 1
c.e : x > 0
se 0 < x²+ (1/2) < 1 ( -√2/2 < x < √2/2) :
2x < x² + (1/2)
x² - 2x + (1/2) > 0
x < (2-√2)/2 ou x > (2+√2)/2
fazendo a interseção : 0 < x < (2-√2)/2 (i)

se x² + (1/2) > 1 ( x < - √2/2 ou x > √2/2 ) :
2x > x² +(1/2)
x² -2x + (1/2) < 0
(2-√2)/2 < x < (2+√2)/2
interseção : √2/2 < x < (2+√2)/2 (ii)
(i) U (ii) :
V = { x ∈ ℝ / 0 < x < (2-√2)/2 ou √2/2 < x < (2+√2)/2 }

Inequação logarítmica

Inequação logarítmica

Re: Inequação logarítmica

Um fórum livre e democrático.