Produtos notáveis

Sabendo que x + y^-1 = 7 e que x = 4y, o valor da expressão x^2 + y^-2 é igual a:

(a) 49
(b) 47
(c) 45
(d) 43
(e) 41

A resposta da questão é a letra e (41), mas gostaria de ter uma resolução clara para a conta.

dede2007 escreveu:Sabendo que x + y^-1 = 7 e que x = 4y, o valor da expressão x^2 + y^-2 é igual a:

(a) 49
(b) 47
(c) 45
(d) 43
(e) 41

A resposta da questão é a letra e (41), mas gostaria de ter uma resolução clara para a conta.

Boa tarde,

Substituindo-se x por 4y, fica:
4y + 1/y = 7
16y² + 1/y² = ?

Elevando ao quadrado a primeira equação, vem:
(4y + 1/y)² = (7)²
(4y)² + 2*4y*1/y + (1/y)² = (7)²

16y² + 8 + 1/y² = 49
16y² + 1/y² = 49 - 8
16y² + 1/y² = 41

Alternativa (e)



Um abraço.

Olá.

x² + y^{-2} = x² + 1/y² .;. (x²y² + 1)/y²

x + y^{-1} = 7 .:. x + 1/y = 7 .:. (x + 1/y)² = 7² .:. x² + 2*x*1/y + 1/y² = 49 .:. x² + 1/y² = 49 - 2x/y .:. x²+1/y² = 49 - 2*(4y)/y .:. x²+1/y² = 41

Att.,
Pedro

mais uma resolução bem simples :
x + 1/y = 7 
Elevando ao quadrado ambos os membros :
(x+1/y)² = 49
x² + 2x/y + 1/y² = 49
Substituindo o valor de x por y :
x²+ 8y/y + 1/y² = 49 >  x² + 1/y² = 41

Obrigado pelas resoluções

Consegui chegar ao resultado estudando a equação de outra maneira, um pouco mais detalhada para quem estiver com dificuldades:

1) O enunciado nos dá duas informações:



2) E nos solicita o resultado de uma equação:



3) Podemos "notar" (daí vem o nome de produtos notáveis) que ele solicita o quadrado da primeira informação que nos deu, ou seja, o resultado será 7² com alguma coisa a mais:



4) Resolvendo a equação:



5) Temos quase o resultado da equação que ele nós solicita, porém a um número no meio nos atrapalhando, que é o:



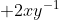
6) Vamos substituir a segunda informação que o enunciado nos deu (x = 4y) para descobrirmos o valor dele:



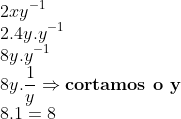
7) Agora tendo o valor da de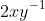 , apenas substituímos na equação do item 4:



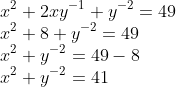
Forte abraço!