Produtos Notáveis
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Produtos Notáveis
Produtos Notáveis
Encontre todos os pares (x , y) de inteiros tais que 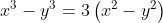 .
.
Tilibra123- Iniciante
- Mensagens : 9
Data de inscrição : 04/12/2014
Idade : 26
Localização : Arcaju-SE, Brasil
 Re: Produtos Notáveis
Re: Produtos Notáveis
Olá, Tilibra123.
x³-y³ = 3(x²-y²) .:. (x-y)(x²+xy+y²) - 3(x-y)(x+y) = 0 .:. (x-y)[x²+y²+xy-3x-3y] = 0 .:. (x-y)[x²+x(y-3)+(y²-3y)] = 0
Para x diferente de y:
x² + x(y-3) + (y²-3y) = 0
Como queremos soluções reais:
(y-3)² - 4*1*(y²-3y) >= 0 .:. y²-6y+9-4y²+12y >= 0 .:. -3y²+6y+9 >= 0 .:. -1 <= y <= 3
Para y = -1: x = (4 +- 0)/2 .:. x = 2
Para y = 0: x = (3 +- 3)/2 .:. x = 0 ou x = 3
Para y = 1, x não é inteiro.
Para y = 2: x = (1 +- 3)/2 .:. x = 2 ou x = -1
Para y = 3: x = (0 +- 0)/2 .:. x = 0
Então, os pares são: (2,-1);(0,0);(3,0);(-1,2);(2;2);(0,3)
Não se esqueça do caso (x,x), que também é solução (x pertencente aos reais).
Att.,
Pedro
x³-y³ = 3(x²-y²) .:. (x-y)(x²+xy+y²) - 3(x-y)(x+y) = 0 .:. (x-y)[x²+y²+xy-3x-3y] = 0 .:. (x-y)[x²+x(y-3)+(y²-3y)] = 0
Para x diferente de y:
x² + x(y-3) + (y²-3y) = 0
Como queremos soluções reais:
(y-3)² - 4*1*(y²-3y) >= 0 .:. y²-6y+9-4y²+12y >= 0 .:. -3y²+6y+9 >= 0 .:. -1 <= y <= 3
Para y = -1: x = (4 +- 0)/2 .:. x = 2
Para y = 0: x = (3 +- 3)/2 .:. x = 0 ou x = 3
Para y = 1, x não é inteiro.
Para y = 2: x = (1 +- 3)/2 .:. x = 2 ou x = -1
Para y = 3: x = (0 +- 0)/2 .:. x = 0
Então, os pares são: (2,-1);(0,0);(3,0);(-1,2);(2;2);(0,3)
Não se esqueça do caso (x,x), que também é solução (x pertencente aos reais).
Att.,
Pedro

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Produtos Notáveis
Re: Produtos Notáveis
Obrigado.
Tilibra123- Iniciante
- Mensagens : 9
Data de inscrição : 04/12/2014
Idade : 26
Localização : Arcaju-SE, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












