(Problema 4) 3º OMCPLP

por Vinícius Santana Qua 05 Mar 2014, 07:04

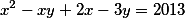Determine todos os pares $(Problema 4) 3º OMCPLP Gera?(x,y)$ de inteiros positivos que satisfazem a equação $(Problema 4) 3º OMCPLP Gera?x^2-xy+2x-3y=2013$ .

por Luck Qua 05 Mar 2014, 16:33

x² - xy + 2x - 3y = 2013
Vamos tentar quebrar em dois fatores:
x² -xy +2x-3y +k = (x+ay+b)(x + c)
x² -xy +2x- 3y+ k = x² + cx + axy +acy +bx + bc
x² -xy +2x- 3y+ k = x² + (c+b)x + axy +acy + bc
a= -1 , c = 3
c + b = 2 ∴ b = -1, bc = k = -3
Então temos:
(x -y-1)(x+3) = 2013 - 3
(x-y-1)(x+3) = 2010
(x-y-1)(x+3) = 2.3.5.67
inteiros positivos:
x+ 3 = 2010 , x-y-1 = 1 ∴ x = 2007 , y = 2005
x+ 3 =3.5.67 , x-y-1 = 2 ∴ x = 1002 , y = 999
x + 3 = 2.5.67 , x-y-1 = 2 ∴ x = 667 , y = 663
x + 3 = 2.3.67 , x-y-1= 2 ∴ x = 399 , y = 393
x+3 = 5.67 , x -y-1 = 6 ∴ x = 332 , y = 325
x + 3 = 3.67 ,x-y-1 = 10 ∴ x = 198 , y = 187
x + 3 = 2.67 ,x - y - 1 = 15 ∴ x = 131 , y = 115
x + 3 = 67 , x -y-1 = 30 ∴ x = 64 , y = 33

S = {(2007,2005) ; (1002,999) ; (667,663); (399,393) ; (332,325) ; (198,187) ; (131,115) ; (64,33) }