Limite - Duas Variáveis (Indeterminação)
2 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
Limite - Duas Variáveis (Indeterminação)
por Convidado Qui 17 Out 2013, 20:48
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Q. 18 - Pág.: 810)
Determine o limite, se existir, ou mostre que não existe.
\rightarrow&space;(0,&space;0)}&space;\frac&space;{xy^4}{x^2+y^8} "\lim_{(x, y)\rightarrow (0, 0)} \frac {xy^4}{x^2+y^8}")
Resposta para o cálculo do limite: 0 (zero).
Coloquei a definição apenas para tentar clarear as ideias. Mas, se alguém conseguir responder por outro método, irá ajudar. Por exemplo, Teorema do Confronto, mudança de variável etc.
Definição de Limite de uma Função de Duas Variáveis (pelo menos):
Expandir esta imagem
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Pág.: 804)
Como faço para provar esse limite?
Determine o limite, se existir, ou mostre que não existe.
Resposta para o cálculo do limite: 0 (zero).
Coloquei a definição apenas para tentar clarear as ideias. Mas, se alguém conseguir responder por outro método, irá ajudar. Por exemplo, Teorema do Confronto, mudança de variável etc.
Definição de Limite de uma Função de Duas Variáveis (pelo menos):
Expandir esta imagem
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Pág.: 804)
Como faço para provar esse limite?
Convidado- Convidado
Re: Limite - Duas Variáveis (Indeterminação)
por Giiovanna Sex 18 Out 2013, 09:26
Note que
Sendo assim,
(é limitada)
E como
Então o limite existe e é zero.
Não sei se você sabe, mas quando temos uma função limitada multiplicada por uma cujo limite vai para zero, então o limite do produto existe e é zero. A afirmação pode ser vista como consequência direta do Teorema do Confronto ou como proposição independente.
Sendo assim,
E como
Então o limite existe e é zero.
Não sei se você sabe, mas quando temos uma função limitada multiplicada por uma cujo limite vai para zero, então o limite do produto existe e é zero. A afirmação pode ser vista como consequência direta do Teorema do Confronto ou como proposição independente.
Giiovanna- Grupo
Velhos amigos do Fórum
- Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Re: Limite - Duas Variáveis (Indeterminação)
por Man Utd Sex 18 Out 2013, 20:39
olá 
a função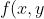=\frac{y^{4}}{x^{2}+y^{8}})
é realmente limitada?
testei o ponto (0,0,1) :
=\frac{(0,1)^{4}}{0^{2}+(0,1)^{8}}&space;\\\\\\&space;f(0,0,1)=\frac{0,0001}{0,00000001}&space;=10000)
a função
testei o ponto (0,0,1) :
Man Utd- Grupo
Velhos amigos do Fórum - Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Limite - Duas Variáveis (Indeterminação)
por Giiovanna Sáb 19 Out 2013, 00:08
Oi,
você tem razão. A última parte da desigualdade não é sempre verdade. Pensarei em uma solução.
Obrigada
você tem razão. A última parte da desigualdade não é sempre verdade. Pensarei em uma solução.
Obrigada
Giiovanna- Grupo
Velhos amigos do Fórum - Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Re: Limite - Duas Variáveis (Indeterminação)
por Man Utd Sáb 19 Out 2013, 08:28
dá pra fazer por coordenadas polares:
\rightarrow&space;(0,0),r\rightarrow&space;0)
então:
então:
Man Utd- Grupo
Velhos amigos do Fórum - Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Limite - Duas Variáveis (Indeterminação)
por Giiovanna Sáb 19 Out 2013, 11:43
Legal sua solução Como eu evito usar coordenadS polares, o que acha dessa tentativa?
Como eu evito usar coordenadS polares, o que acha dessa tentativa?
Giiovanna- Grupo
Velhos amigos do Fórum - Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Re: Limite - Duas Variáveis (Indeterminação)
por Man Utd Sáb 19 Out 2013, 12:29
olá.
eu acho que
, tbm não é limitada,ao meu ver somente 
é limitada,é bem fácil ver usando coordenadas polares :
}{2})
, Im(f)=[-1/2,1/2]
então se a função fosse assim
, poderíamos usar o teorema da função limitada.
eu acho que
então se a função fosse assim
Man Utd- Grupo
Velhos amigos do Fórum - Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Limite - Duas Variáveis (Indeterminação)
por Giiovanna Sáb 19 Out 2013, 16:00
Oi Man, o que há de errado, então?
Neste caso, a desigualdade parece perfeitamente correta (na outra havia um erro mesmo).
O resultado confere no wolfram. (Neste caso, coloquei uma outra função por cima, não um único valor. Os valores perto do 0 ainda pode ser grandes)
, pois y^8 >= 0
Como |x| >= 0, então
, o que é perfeitamente razoável pois y^8 >= 0 e x^2 = |x^2|
Então,
Não vejo o que pode estar, conceitualmente, errado.
Talvez fique mais claro ver como
Neste caso, a desigualdade parece perfeitamente correta (na outra havia um erro mesmo).
O resultado confere no wolfram. (Neste caso, coloquei uma outra função por cima, não um único valor. Os valores perto do 0 ainda pode ser grandes)
Como |x| >= 0, então
Então,
Não vejo o que pode estar, conceitualmente, errado.
Talvez fique mais claro ver como
Giiovanna- Grupo
Velhos amigos do Fórum - Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Re: Limite - Duas Variáveis (Indeterminação)
por Man Utd Sáb 19 Out 2013, 16:26
olá .
Tbm não sei dizer o que está errado.
mas a função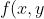=\frac{x}{x^{2}+y^{8}})
, não é limitada.
=\frac{0,1}{(0,1)^{2}+0^{8}}&space;\\\\&space;f(0,1,0)=\frac{0,1}{0,01}=10)
.Tbm não sei dizer o que está errado.
mas a função
Man Utd- Grupo
Velhos amigos do Fórum - Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Limite - Duas Variáveis (Indeterminação)
por Giiovanna Sáb 19 Out 2013, 16:33
Hm, neste caso a desigualdade está correta, só não está correto o que eu queria fazer mesmo
Giiovanna- Grupo
Velhos amigos do Fórum - Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Página 1 de 2 • 1, 2
Tópicos semelhantes» Limite com duas variáveis.
» Limite, duas variavéis.
» LIMITE COM DUAS VARIÁVEIS
» Limite de duas variáveis
» Limite de Duas Variáveis
» Limite, duas variavéis.
» LIMITE COM DUAS VARIÁVEIS
» Limite de duas variáveis
» Limite de Duas Variáveis
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
