Demonstração em polinômio

por Davi Cesar Correia Jr. 10/10/2013, 12:36 pm

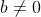Considere o polinômio $Demonstração em polinômio Gif$ de coeficientes reais, com $Demonstração em polinômio Gif$ . Sabendo que suas raízes são reais, demonstre que a < 0.

por Luck 10/10/2013, 2:21 pm

Girard:
x1x2 + x2x3 + x1x3 = a
x1 + x2 + x3 = 0∴ (x1+x2+x3)² = 0
x1² + x2² + x3² + 2(x1x2 + x2x3+x1x3) = 0
x1² + x2² + x3² +2a = 0 ∴ a = -(x1²+x2²+x3²)/2 como b# 0 o polinômio nao é nulo , então x1,x2,x3#0 , logo a < 0 c.q.d

por Davi Cesar Correia Jr. 11/10/2013, 11:09 am

Ok, eu entendi, muito obrigado!!
Mas, só uma coisa que não ficou muito clara pra mim: qual seria o "problema" se b fosse nulo? O que isso implicaria? E o que, ou como, o fato de b # 0 confirma sua solução?

por Luck 11/10/2013, 12:56 pm

Davi Cesar Correia Jr. escreveu:Ok, eu entendi, muito obrigado!!
Mas, só uma coisa que não ficou muito clara pra mim: qual seria o "problema" se b fosse nulo? O que isso implicaria? E o que, ou como, o fato de b # 0 confirma sua solução?

se b =0, o polinômio poderia ser nulo, e daí x1=x2=x3 = 0 ,o que daria a = 0 .. nao seria necessária esta condição se ele pedisse para provar que a ≤ 0.