Numa urna

por Chronoss Dom 6 Out - 20:13

Numa urna há 10 bolas brancas e 10 bolas pretas.

1º) Calcule o número , Kρ , de maneiras para que se possa extrair da urna 10 bolas , das quais p são pretas ( 0 ≤ p ≤ 10 )

2º) Calcule a soma : $\large N\: =\: \sum_{p=0}^{10}k_{p}$

Gabarito:

por Chronoss Ter 8 Out - 6:29

por **Giiovanna** Ter 8 Out - 8:56

a) Para que eu extraia 10 bolas, em que exatamente p são pretas, eu preciso:

a) Extrair p bolas pretas e
b) Extrair 10-p bolas brancas

Portanto há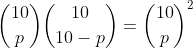 $Numa urna Gif$ maneiras de extrair as bolas

(uma melhor analogia seria pensar que você vai escolher p lugares para por p bolas pretas e 10-p para por bolas brancas. Nesse caso, vê-se , claramente, a necessidade de usar combinatória )

b) Ainda não pensei em uma boa maneira de cálcular isso (tirando fazer na mão)

por **Robson Jr.** Ter 8 Out - 10:41

No item b, queremos a soma:

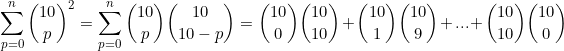
$\small \sum_{p=0}^{10} \binom{10}{p}^2=\sum_{p=0}^{10} \binom{10}{p}\binom{10}{10-p}=\binom{10}{0}\binom{10}{10}+\binom{10}{1}\binom{10}{9}+...+\binom{10}{10}\binom{10}{0}$

Suponha o seguinte problema: de quantas maneiras podemos sacar 10 bolas de uma urna que contém 10 bolas pretas e 10 bolas brancas? Ora, podemos sacar 0 de 10 bolas pretas e 10 de 10 bolas brancas, ou 1 de 10 bolas pretas e 9 de 10 bolas brancas, ou 2 de 10 bolas pretas e 8 de 10 bolas brancas, ou ..., ou 10 de 10 bolas pretas e 0 de 10 bolas brancas. Somando todas as possibilidades, temos exatamente o somatório pedido.

Poderíamos, porém, resolver o mesmo problema de outra forma mais simples: bastaria tomar 10 bolas dentre 20.

Como ambas as contagens precisam levar ao mesmo resultado:

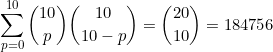
$\small \sum_{p=0}^{10} \binom{10}{p}\binom{10}{10-p}=\binom{20}{10}= 184756$

por Chronoss Ter 8 Out - 14:09

Obrigado aos dois.

Para mim o enunciado descreve um situação bem confusa , pois não foi estabelecido dentre os elementos de um mesmo conjunto características que os distinguem , logo enumerar as combinações de 10 elementos , tomando p elementos do conjunto P { Bolas pretas } e 10-p elementos do conjunto B { Bolas brancas } seria impraticável se fosse :

$\large P\: =\: \left \{ \bullet ;\bullet ;\bullet ;\bullet ;\bullet ; \bullet ;\bullet ;\bullet ;\bullet ;\bullet \right \}$

$\large B\; =\: \: \left \{ \circ ;\circ ;\circ ;\circ ;\circ ;\circ ;\circ ;\circ ;\circ ;\circ \right \}$

Deveria ser algo como :

$\large P\: =\: \left \{ \bullet _{1} ;\bullet _{2} ;\bullet _{3} ;\bullet _{4} ;\bullet _{5} ;\bullet _{6} ;\bullet _{7} ;\bullet _{8} ;\bullet _{9} ;\bullet _{10} \right \}$

$\large B\; =\: \: \left \{ \circ _{1} ;\circ _{2} ;\circ _{3} ;\circ _{4} ;\circ _{5} ;\circ _{6} ;\circ _{7} ;\circ _{8} ;\circ _{9} ;\circ _{10} \right \}$

Assim poderíamos distinguir uma combinação formada com p elementos de P e 10-p elementos de B de outra com o mesmos números de elementos de P e B, por exemplo as combinações com 3 elementos de P e 7 elementos de B seriam todas iguais se não tivesse distinção entre os elementos do mesmo.

Concordam com essa interpretação ?

por **Robson Jr.** Ter 8 Out - 17:42

À rigor, o enunciado não disse "bolas pretas idênticas". Nesse caso, por mais estranho que pareça, é equivocado supor que quaisquer elementos sejam idênticos entre si. A intenção do elaborador da questão certamente foi que as bolas fossem consideradas não-idênticas, o que é reforçado pelas respostas do exercício.

Ademais, perceba que, se as bolas de mesma cor de fato fossem indistinguíveis entre si, o problema perderia o sentido. Afinal, se tenho 10 bolas pretas idênticas e 10 bolas brancas idênticas, o número de maneiras de sacar p bolas pretas da urna é 1, independente do p.

Uma maneira mais coerente de redigir o problema seria, por exemplo, substituir "bolas pretas" e "bolas brancas" por "homens" e "mulheres". Observe:

"Numa sala, estão presentes 10 homens e 10 mulheres. Calcule o número Kp de maneiras de selecionar 10 pessoas nessa sala, das quais p são homens"

Como seria absurda a ideia de trabalhar com clones, acredito que essa reformulação causaria menos estranheza.

por Chronoss Ter 8 Out - 19:01

Concordo ,mas também não podemos concluir que elas são distinguíveis somente pelos dados apresentados , na minha opinião o enunciado está formulado erroneamente .

A rigor , pelo ponto de vista dedutivo formal concluiríamos que a questão demonstra ambiguidade, logo ambas as respostas seriam validas ; e pelo ponto de vista experimental concluiríamos que não há informações suficientes para realizar o processo de contagem ( uma alternativa seria manipular as características do elementos dos conjuntos do experimento , tornando-os contáveis , parecido com oque vc fez ) .

rsrs viajei legal. Razz

por Conteúdo patrocinado

Numa urna

Numa urna

Re: Numa urna

Re: Numa urna

Re: Numa urna

Re: Numa urna

Re: Numa urna

Re: Numa urna

Re: Numa urna

Um fórum livre e democrático.