cilindro de madeira
3 participantes
PiR2 :: Física :: Mecânica dos Fluidos
Página 1 de 1
 cilindro de madeira
cilindro de madeira
Ao brincar com um cilindro de madeira de densidade mc e altura h, em um tanque com água de densidade ma, você perceberá que o cilindro flutua, em equilíbrio, conforme indica a figura I. Caso você dê um leve toque na face superior e emersa (figura II), notará que o cilíndro, após imergir uma certa profundidade, oscilará por algum tempo, sujeito a uma força restauradora de intensidade do tipo F = kx, tal qual um oscilador harmônico típico.
A aplicação do modelo de um oscilador harmônico simples é bastante razoável para se descrever o movimento de sobe e desce do cilindro, sujeito ao campo gravitacional g, se a água for considerada um líquido ideal. Tendo por base essa situação, pode-se prever que o período de oscilação do cilindro é


A aplicação do modelo de um oscilador harmônico simples é bastante razoável para se descrever o movimento de sobe e desce do cilindro, sujeito ao campo gravitacional g, se a água for considerada um líquido ideal. Tendo por base essa situação, pode-se prever que o período de oscilação do cilindro é


Bruno Barreto- Mestre Jedi

- Mensagens : 997
Data de inscrição : 23/10/2009
Idade : 34
Localização : Pernambuco
 Re: cilindro de madeira
Re: cilindro de madeira
O período de um oscilador harmônico é dado por: 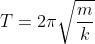 em que k é a constante do oscilador (mola) em N/m. É essa constante que devemos encontrar.
em que k é a constante do oscilador (mola) em N/m. É essa constante que devemos encontrar.
Na condição de equilíbrio E=P e como a área da seção do cilindro é constante, o empuxo vai aumentar proporcionalmente a cada incremento na altura mergulhada.
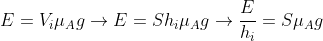
agora temos aí uma grandeza que tem a dimensão (N/m) procurada
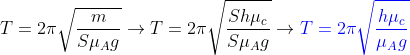
Na condição de equilíbrio E=P e como a área da seção do cilindro é constante, o empuxo vai aumentar proporcionalmente a cada incremento na altura mergulhada.
agora temos aí uma grandeza que tem a dimensão (N/m) procurada
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: cilindro de madeira
Re: cilindro de madeira
#PeloFimDaCarteação rs
Segue a solução:
Quando existir um MHS, teremos que:
E - P = m(w^2)r
Vamos supor que o deslocamento do cilindro seja um dx minúsculo. Ele é a amplitude do nosso MHS e consequentemente o raio do nosso MCU, a nossa interpretação do MHS.
Seja y a altura submersa do cilindro na posição de equilíbrio, antes de darmos o leve toquinho nele
(y + dx).S.μa.g - S.h.μc.g = S.h.μc.(w^2).dx
Mas no equilíbrio
S.μa.y.g = S.μc.h.g
y = μc . h / μa
Substituindo esse y na expressão lá de cima, poderemos dividir os dois lados por dx depois de uma pequena álgebra que não vou colocar aqui
Daí encontramos que w = raiz de (g.μa)/(h.μc)
Como T = 2pi/w
Encontramos o período
Segue a solução:
Quando existir um MHS, teremos que:
E - P = m(w^2)r
Vamos supor que o deslocamento do cilindro seja um dx minúsculo. Ele é a amplitude do nosso MHS e consequentemente o raio do nosso MCU, a nossa interpretação do MHS.
Seja y a altura submersa do cilindro na posição de equilíbrio, antes de darmos o leve toquinho nele
(y + dx).S.μa.g - S.h.μc.g = S.h.μc.(w^2).dx
Mas no equilíbrio
S.μa.y.g = S.μc.h.g
y = μc . h / μa
Substituindo esse y na expressão lá de cima, poderemos dividir os dois lados por dx depois de uma pequena álgebra que não vou colocar aqui
Daí encontramos que w = raiz de (g.μa)/(h.μc)
Como T = 2pi/w
Encontramos o período
RafaelSchuinki- Iniciante
- Mensagens : 27
Data de inscrição : 19/04/2019
Idade : 24
Localização : Ponta Grossa, Paraná, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Geometria Espacial - Cilindro - volume do cilindro
» Um bloco de madeira
» Volume da Madeira
» Uma caixa de madeira
» Ripa de madeira
» Um bloco de madeira
» Volume da Madeira
» Uma caixa de madeira
» Ripa de madeira
PiR2 :: Física :: Mecânica dos Fluidos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












