Teoria dos números primos

por Lucca Sex 13 Set - 8:44

Bom dia
Queria saber resolver esta questão
Quantas vezes o fator primo 11 aparece na decomposição do produto gerado por 100x101x...x1001
Eu achei 98 mas o gabarito esta falando q é 89

por **Elcioschin** Sex 13 Set - 16:41

Múltiplos de 11 ----> 110, 121, 132 ................ 1 001

PA ----> a1 = 110, an = 1 001. r = 11

an = a1 + (n - 1).r ----> 1 001 = 110 + (n - 1).11 ----> n = 82

por **fantecele** Sex 13 Out - 12:58

Mestre Elcio, nesse questão você deve analisar também que haverá números que terão expoente ao quadrado para o 11, então deve ser contado mais de uma vez e seriam eles os números 121 vezes 1, 2, ..., 7 e 8, com isso a resposta seria 82 + 8 = 90.

Uma outra forma de fazer seria usar o seguinte teorema:

"O expoente de um primo p na fatoração, em fatores primos, de n!, onde n é um número natural, é:
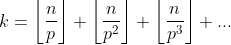
$k=\left \lfloor \frac{n}{p} \right \rfloor+\left \lfloor \frac{n}{p^2} \right \rfloor+\left \lfloor \frac{n}{p^3} \right \rfloor+...$

Dessa forma, multiplicando e dividindo o número 100x101x...x1001 por 99! iremos ficar com 1001!/99!, com isso, temos que a quantidade que o fator primo 11 aparece é igual a quantidade de vezes que ele aparece em 1001! menos a quantidade de vezes que ele aparece em 99!, dessa forma:

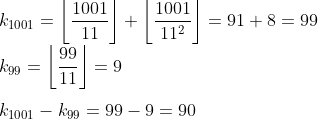
$\\k_{1001}=\left \lfloor \frac{1001}{11} \right \rfloor+\left \lfloor \frac{1001}{11^2} \right \rfloor=91+8=99\\k_{99}=\left \lfloor \frac{99}{11} \right \rfloor=9\\\\k_{1001}-k_{99}=99-9=90$