UNESP - 1ª Fase
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
UNESP - 1ª Fase
por Curitibana Sex 06 Set 2013, 11:00
Sabe-se que a função quadrática f(x) = ax² + bx + c possui duas raízes reais 
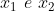, satisfazendo 
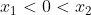. Nessas condições, podemos afirmar que:
R.: a.c < 0
Gostaria de uma ajuda com essa questão, obrigada
R.: a.c < 0
Gostaria de uma ajuda com essa questão, obrigada
Curitibana- Recebeu o sabre de luz
- Mensagens : 117
Data de inscrição : 07/09/2012
Idade : 31
Localização : Curitiba, Paraná, Brasil
Re: UNESP - 1ª Fase
por Elcioschin Sex 06 Set 2013, 18:05
x = [- b ± \/(b² - 4ac)]/2a
Para uma raiz ser positiva e a outra negativa devemos ter:
- b + \/(b² - 4ac) > 0 ----> b² < b² - 4ac ----> 0 < - 4ac ----> ac < 0
Para uma raiz ser positiva e a outra negativa devemos ter:
- b + \/(b² - 4ac) > 0 ----> b² < b² - 4ac ----> 0 < - 4ac ----> ac < 0
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» UNESP 2ª fase - Álgebra
» (Unesp-2ª fase) Progressão Aritmética
» UNESP 2ª fase
» Unesp 1ª fase/2015
» Unesp 2012 - 1ª fase
» (Unesp-2ª fase) Progressão Aritmética
» UNESP 2ª fase
» Unesp 1ª fase/2015
» Unesp 2012 - 1ª fase
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
