Eletrostática
4 participantes
Página 1 de 1
 Eletrostática
Eletrostática
Uma mola ideal de constante elástica k se encontra no interior de um tubo vertical presa pela sua extremidade inferior. Sobre sua extremidade superior, encontra-se, em repouso, uma pequena esfera de massa m e carga elétrica positiva q . A esfera se ajusta perfeitamente ao interior do tubo e pode deslizar sobre a parede lateral do tubo sem atrito. A esfera, o tubo e a mola são formados de materiais dielétricos. O módulo da aceleração da gravidade local é g.
a) Determine a deformação sofrida pela mola.

Um campo elétrico uniforme vertical de sentido para baixo é aplicado ao interior do tubo com sua intensidade sendo aumentada muito lentamente até o valor Eo
b) Determine a nova deformação da mola.

A intensidade do campo elétrico, então, é subitamente levada à zero.
c) Considerando que a esfera não estava presa à extremidade superior da mola, calcule a altura máxima atingida pela esfera a partir de sua posição no instante em que o campo elétrico é anulado.
d) Considerando que a esfera está presa à extremidade superior da mola, determine a frequência e a amplitude do movimento harmônico simples que passa a executar o sistema esfera-mola.
Resp.:
a) xo = mg/k
b) x'o = (mg+q*Eo)/k
c) h = (mg+qEo)^2/2kmg
d) f = 1/2∏*√(k/m)
A = (q*Eo)/k
se possível, peço que alguém possa me ajudar na letra D resolvendo-a a partir da lei da conservação de energia.
a) Determine a deformação sofrida pela mola.

Um campo elétrico uniforme vertical de sentido para baixo é aplicado ao interior do tubo com sua intensidade sendo aumentada muito lentamente até o valor Eo
b) Determine a nova deformação da mola.

A intensidade do campo elétrico, então, é subitamente levada à zero.
c) Considerando que a esfera não estava presa à extremidade superior da mola, calcule a altura máxima atingida pela esfera a partir de sua posição no instante em que o campo elétrico é anulado.
d) Considerando que a esfera está presa à extremidade superior da mola, determine a frequência e a amplitude do movimento harmônico simples que passa a executar o sistema esfera-mola.
Resp.:
a) xo = mg/k
b) x'o = (mg+q*Eo)/k
c) h = (mg+qEo)^2/2kmg
d) f = 1/2∏*√(k/m)
A = (q*Eo)/k
se possível, peço que alguém possa me ajudar na letra D resolvendo-a a partir da lei da conservação de energia.
gabrielfe26- Iniciante
- Mensagens : 34
Data de inscrição : 09/03/2013
Idade : 28
Localização : es
 Re: Eletrostática
Re: Eletrostática
No momento inicial, temos apenas a força peso fazendo uma distensão na mola, sendo seu comprimento neste equilíbrio x0:
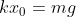
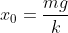
b) Quando ele diz que vai aumentando o valor lentamente, ele quer dizer que quando tiver no último valor, ele vai atingir um novo equilíbrio :
=mg+qE_0)
=\frac{mg+qE_0}{k})
c) Como encontramos a deformação (x0-x'0), a energia mecânica se conservará no ponto mais alto:
^2}{2}=mgh)
^2}{k^2}=2mgh)
^2}{2mgk}=h)
d) Considerando que o campo elétrico se anule nesse ponto, temos que:
-mg=ma)
Como encontramos kx0 no item a, poderemos substituí-lo:
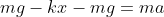
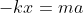
Nisto, encontramos a equação fundamental do M.H.S, provando o movimento do sistema, com isso, podemos achar a frequência angular:

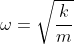
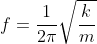
Para acharmos A, bastamos saber que a força restauradora será máxima quando x for A:
k(x0-x'0)-mg=kA
Como descobrimos k(x0-x'0), bastamos substituir:
mg+qE0-mg=kA
A=qE0/k
b) Quando ele diz que vai aumentando o valor lentamente, ele quer dizer que quando tiver no último valor, ele vai atingir um novo equilíbrio :
c) Como encontramos a deformação (x0-x'0), a energia mecânica se conservará no ponto mais alto:
d) Considerando que o campo elétrico se anule nesse ponto, temos que:
Como encontramos kx0 no item a, poderemos substituí-lo:
Nisto, encontramos a equação fundamental do M.H.S, provando o movimento do sistema, com isso, podemos achar a frequência angular:
Para acharmos A, bastamos saber que a força restauradora será máxima quando x for A:
k(x0-x'0)-mg=kA
Como descobrimos k(x0-x'0), bastamos substituir:
mg+qE0-mg=kA
A=qE0/k

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Re: Eletrostática
Re: Eletrostática
Muito bom, VictorCoe, explicado com clareza, ordem e paciência.
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Eletrostática
Re: Eletrostática
Obrigado por ter respondido, VictorCoe! Uma dúvida, eu poderia afirmar direto que a frequência é 1/2∏*√(k/m), certo?
gabrielfe26- Iniciante
- Mensagens : 34
Data de inscrição : 09/03/2013
Idade : 28
Localização : es
 Re: Eletrostática
Re: Eletrostática
A demonstração do Victor foi bastante completa, ainda não tinha visto assim.gabrielfe26 escreveu:Obrigado por ter respondido, VictorCoe! Uma dúvida, eu poderia afirmar direto que a frequência é 1/2∏*√(k/m), certo?
Mas Gabriel, em questões assim, dá pra afirmar direto que a frequência é essa, pois é uma das equações principais do MHS. Não teria problema partir dela numa prova.
Gabriel Rodrigues- Matador

- Mensagens : 1148
Data de inscrição : 08/02/2013
Idade : 28
Localização : São Carlos, SP
 Re: Eletrostática
Re: Eletrostática
A demonstração do Victor foi bastante completa, ainda não tinha visto assim.gabrielfe26 escreveu:Obrigado por ter respondido, VictorCoe! Uma dúvida, eu poderia afirmar direto que a frequência é 1/2∏*√(k/m), certo?
Mas Gabriel, em questões assim, dá pra afirmar direto que a frequência é essa, pois é uma das equações principais do MHS. Não teria problema partir dela numa prova.
Gabriel Rodrigues- Matador

- Mensagens : 1148
Data de inscrição : 08/02/2013
Idade : 28
Localização : São Carlos, SP
 Re: Eletrostática
Re: Eletrostática
Beleza então, obrigado pelas respostas e pela atenção!
gabrielfe26- Iniciante
- Mensagens : 34
Data de inscrição : 09/03/2013
Idade : 28
Localização : es
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












