OBF 2011
5 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Física
Página 1 de 2
Página 1 de 2 • 1, 2 
 OBF 2011
OBF 2011
Uma bolha de gas, inicialmente com pressao interna P0 e volume V0 e mantida em equilibrio
estático dentro de um lago cuja densidade é p .Num dado instante a bolha é levemente perturbada e inicia um
movimento acelerado. Considerando que a temperatura da bolha é praticamente constante e que a
aceleração da gravidade local e g, determine a energia cinética da mesma quando ela subir uma pequena
altura h. Desconsidere efeitos de tensão superficial e, se necessário, utilize (1+x) elevado a n = 1+nx, se x <<1
.
estático dentro de um lago cuja densidade é p .Num dado instante a bolha é levemente perturbada e inicia um
movimento acelerado. Considerando que a temperatura da bolha é praticamente constante e que a
aceleração da gravidade local e g, determine a energia cinética da mesma quando ela subir uma pequena
altura h. Desconsidere efeitos de tensão superficial e, se necessário, utilize (1+x) elevado a n = 1+nx, se x <<1
.
icepalace- Iniciante
- Mensagens : 5
Data de inscrição : 02/08/2013
Idade : 29
Localização : BR
 Re: OBF 2011
Re: OBF 2011
Eu acho que tive uma ideia, mas não consegui terminar.
O problema pede Ec = f{Po, Vo, p, g, h}.
Desconsiderando a pressão atmosférica no local (já que não foi feita nenhuma menção à mesma), tem-se, pelo teorema de Stevin, que a pressão que age na bolha é dada por P = p.g.D, onde 'D' é a altura da coluna de líquido sobre a bolha.
Assim, admitindo que a bolha está, inicialmente, localizada a uma profundidade H, tem-se: Po = p.g.H -> (eq1) e
P = p.g.(H - h) -> (eq2).
Considerando que as únicas forças que agem na bolha são o Empuxo de Arquimedes e o peso da bolha, tem-se, pelo teorema da Energia cinética:
W(E->) + W(P->) = Ec => Ec = W(E->) - m.g.h -> (eq3).
Agora há um problema: O Empuxo que age na bolha (dado pelo teorema de Arquimedes: |E->| = p.V.g) é variável, pois o volume da bolha é variável, logo, para calcular o trabalho realizado por esse Empuxo, devemos calcular a integral

Para isso, considere a Lei de Boyle (já que a temperatura é constante):
P.V = Po.Vo => (eq1) e (eq2): p.g.(H - h).V = p.g.H.Vo <=> V = [H/(H - h)].Vo -> (eq5).
Substituindo (eq5) em (eq4), obtém-se:

Do equilíbrio estático inicial, tem-se p.Vo.g = m.g <=> m = p.Vo -> (eq6).
Substituindo (eq6) e a expressão deduzida para W(E->) em (eq3), vem:
Ec = p.Vo.g.(H.In(H - h) - h).
Daí, não consigo tirar esse 'H' dali (nem sei se o que eu fiz está certo...).
O problema pede Ec = f{Po, Vo, p, g, h}.
Desconsiderando a pressão atmosférica no local (já que não foi feita nenhuma menção à mesma), tem-se, pelo teorema de Stevin, que a pressão que age na bolha é dada por P = p.g.D, onde 'D' é a altura da coluna de líquido sobre a bolha.
Assim, admitindo que a bolha está, inicialmente, localizada a uma profundidade H, tem-se: Po = p.g.H -> (eq1) e
P = p.g.(H - h) -> (eq2).
Considerando que as únicas forças que agem na bolha são o Empuxo de Arquimedes e o peso da bolha, tem-se, pelo teorema da Energia cinética:
W(E->) + W(P->) = Ec => Ec = W(E->) - m.g.h -> (eq3).
Agora há um problema: O Empuxo que age na bolha (dado pelo teorema de Arquimedes: |E->| = p.V.g) é variável, pois o volume da bolha é variável, logo, para calcular o trabalho realizado por esse Empuxo, devemos calcular a integral

Para isso, considere a Lei de Boyle (já que a temperatura é constante):
P.V = Po.Vo => (eq1) e (eq2): p.g.(H - h).V = p.g.H.Vo <=> V = [H/(H - h)].Vo -> (eq5).
Substituindo (eq5) em (eq4), obtém-se:

Do equilíbrio estático inicial, tem-se p.Vo.g = m.g <=> m = p.Vo -> (eq6).
Substituindo (eq6) e a expressão deduzida para W(E->) em (eq3), vem:
Ec = p.Vo.g.(H.In(H - h) - h).
Daí, não consigo tirar esse 'H' dali (nem sei se o que eu fiz está certo...).
![JOAO [ITA]](https://2img.net/u/2713/85/25/58/avatars/20221-80.jpg)
JOAO [ITA]- Fera

- Mensagens : 866
Data de inscrição : 25/02/2012
Idade : 27
Localização : São José dos Campos,SP,Brasil
 Re: OBF 2011
Re: OBF 2011
João, olhe a minha resolução, não sei se está certa, mas vamos lá.
I) Primeiramente, no equilíbrio estático, temos que mg=p.V0.g.
II) Com isso, podemos criar um gráfico de E x D , em que é o empuxo versus distância (é quase a mesma coisa deste gráfico, invés de P x V, é E x D, e o ponto A começa onde x=0, mas E é diferente de zero, pois no ponto referencial onde x=0, E=mg):
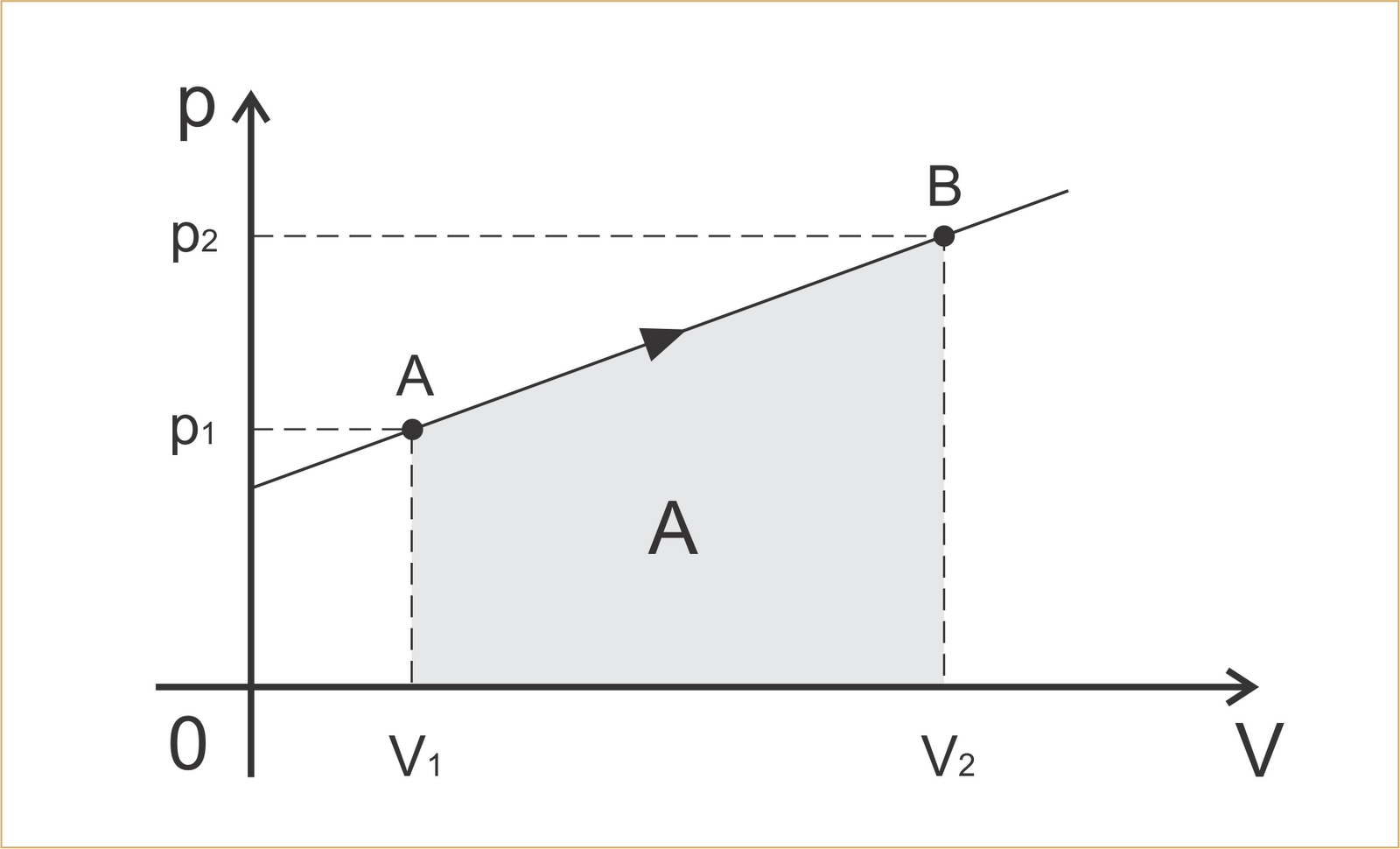
III) Nisto, sabemos que a área do gráfico nos dará o trabalho dado, então:
h}{2})
h}{2})
}{2})
Mas não sabemos V.
IV) Por lei de Boyle, sabemos que :
Mas também sabemos que pelo teorema de Stevin que (como ele não fala da pressão atmosférica, deixei como desprezível) :


Subtraindo a equação encontramos)
(H-x)=h(que é a altura que ele sobe)


Agora que achamos P, podemos achar V :


V)}{2})
)
)
}{(P_0-\rho&space;gh)}&space;\right)
}{2(P_0-\rho&space;gh)}&space;\right)
VI) agora bastamos encontrar a energia cinética da bolha:


}-mgh=E_C)
}-\rho&space;V_0gh=E_C)
I) Primeiramente, no equilíbrio estático, temos que mg=p.V0.g.
II) Com isso, podemos criar um gráfico de E x D , em que é o empuxo versus distância (é quase a mesma coisa deste gráfico, invés de P x V, é E x D, e o ponto A começa onde x=0, mas E é diferente de zero, pois no ponto referencial onde x=0, E=mg):

III) Nisto, sabemos que a área do gráfico nos dará o trabalho dado, então:
Mas não sabemos V.
IV) Por lei de Boyle, sabemos que :
Mas também sabemos que pelo teorema de Stevin que (como ele não fala da pressão atmosférica, deixei como desprezível) :
Subtraindo a equação encontramos
(H-x)=h(que é a altura que ele sobe)
Agora que achamos P, podemos achar V :
V)
VI) agora bastamos encontrar a energia cinética da bolha:

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Re: OBF 2011
Re: OBF 2011
Boa sacada sua para calcular o volume final em função dos dados fornecidos.
Mas, observe a expressão para o cálculo do Empuxo e veja como ela varia com 'h': |E->| = p.V.g =>
=>|E->| = (p.Po.Vo.g)/(Po - p.g.h) -> (*).
A expressão (*) certamente não é a equação de uma reta (se considerarmos a função E(h)), logo o uso de Cálculo Integral me parece inevitável.
Usando a expressão que você encontrou para o cálculo do volume final na (eq4) da minha mensagem anterior, teríamos:

Ainda estou um pouco inseguro por não ter precisado usar a aproximação (1 + x)^n ≈ 1 + n.x, x << 1 que foi fornecida no enunciado.
Mas, observe a expressão para o cálculo do Empuxo e veja como ela varia com 'h': |E->| = p.V.g =>
=>|E->| = (p.Po.Vo.g)/(Po - p.g.h) -> (*).
A expressão (*) certamente não é a equação de uma reta (se considerarmos a função E(h)), logo o uso de Cálculo Integral me parece inevitável.
Usando a expressão que você encontrou para o cálculo do volume final na (eq4) da minha mensagem anterior, teríamos:

Ainda estou um pouco inseguro por não ter precisado usar a aproximação (1 + x)^n ≈ 1 + n.x, x << 1 que foi fornecida no enunciado.
![JOAO [ITA]](https://2img.net/u/2713/85/25/58/avatars/20221-80.jpg)
JOAO [ITA]- Fera

- Mensagens : 866
Data de inscrição : 25/02/2012
Idade : 27
Localização : São José dos Campos,SP,Brasil
 Re: OBF 2011
Re: OBF 2011
Hm, talvez você tenha a razão. Queria arranjar um jeito de encontrar uma solução sem cálculo.

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Re: OBF 2011
Re: OBF 2011
Eu achei estranho ter que usar Cálculo em uma questão da 2ª fase da OBF (tá certo que às vezes eles cobram umas questões que tem que usar, mas isso só para o 3º ano e na 3ª fase).
![JOAO [ITA]](https://2img.net/u/2713/85/25/58/avatars/20221-80.jpg)
JOAO [ITA]- Fera

- Mensagens : 866
Data de inscrição : 25/02/2012
Idade : 27
Localização : São José dos Campos,SP,Brasil

Kongo- Elite Jedi

- Mensagens : 916
Data de inscrição : 22/01/2011
Idade : 30
Localização : Juiz de Fora - MG
 Re: OBF 2011
Re: OBF 2011
Talvez, se usássemos o fato que a isoterma que faria no gráfico fosse uma reta, ficaria mais "bonitinho", pelo fato de que h é muito pequeno... 

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
 Re: OBF 2011
Re: OBF 2011
Isso é bem razoável.VictorCoe escreveu:Talvez, se usássemos o fato que a isoterma que faria no gráfico fosse uma reta, ficaria mais "bonitinho", pelo fato de que h é muito pequeno...
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: OBF 2011
Re: OBF 2011
Então minhas equações estão corretas ? Provavelmente, mas o método do João por cálculo seria o mais correto.

VictorCoe- Fera

- Mensagens : 530
Data de inscrição : 20/02/2012
Idade : 27
Localização : Fortaleza/Ceará
Página 1 de 2 • 1, 2 
PiR2 :: Questões Especiais :: Olimpíadas :: Física
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












