Distribuição Binomial

Uma variável aleatória com distribuição binomial tem a função repartição dada por:

F(0) = 1/243 F(3) = 131/243
F(1) = 11/243 F(4) = 211/243
F(2) = 51/243 F(5) = 1
Determinar:
A) n
B) p e q
C) media de Y
D) variância de Y
E) P(u >= 1)

Define-se função repartição ou função distribuição acumulada da variável aleatória discreta X da seguinte maneira:



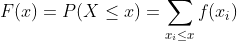
Em que, nesse caso, 

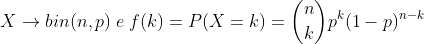
, em que 0<=k <= n

(a) Como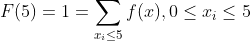 , em que xi é um número natural, temos que n=5, pois a f(x) é função de probabilidade se, e somente se, 

, isso por que sabemos que F(4) não é 1 (pois, se fosse, n seria 4 se F(3) não fosse 1)

(b)

Temos que:



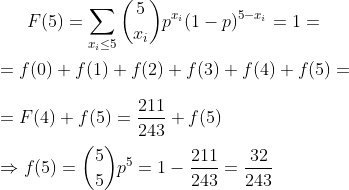
Que número p, maior que zero e menor que 1, elevado a quinta da 32/243?

2^5 = 32 e 3^5 = 243

Assim, p = 2/3 e q = 1-p = 1/3

Você poderia usar F(0) para descobrir q e depois p, da na mesma.

(c) 



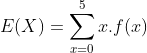
Mas, como a X ~ bin(n,p) = binom(5, 2/3), temos que 

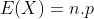, e portanto, E(X) = 10/3

(Se você não conhece essa fórmula, ela é obtida quando escrevemos a X como uma soma de 5 ( ou melhor, n) variáveis aleatórias Z_i i.i.d tal que Z ~ ber(p), em que ber é a distribuição Bernouilli)

(d) 
O mesmo para a variância:
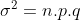, só calcular.

A última você faz, já tem todos os dados ai

Se você não soubesse as fórmulas para C e D, bastaria calcular da forma comum, certo?

Até

Seria legal você colocar o gabarito da próxima vez.

Giiovanna ta certinho, gostei, vc me explicou muito passo a passo, obrigado, na ultima e) P(u>= 1) então seria os valores maiores e igual a 1, então ficaria p= 1 - p(0), 1 - 1/243 = 242/243

Isso

Giiovanna, e se fosse p( 2< x < 4)? Gabarito é 200/243