Conjuntos

Como provar que 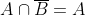 se, e somente se  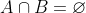, sem usar o diagrama de Venn?

Podemos fazer pensando. Como é "se, e somente se", temos que fazer a ida e a volta, né? Vou chamar o complemento de B de B^c, ok?

(=>) Vamos supor que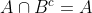  . Então, isso significa que . 

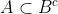Ora, mas se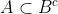 , então se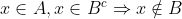 

Portanto,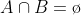 

( <= ) Supomos que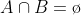 . Ou seja, se x é um elemento tal que 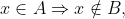, para todo x pertencente ao conjunto A. Mas, por definição de complemento de um conjunto, se z é um elemento tal que . 

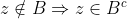Então, se isso é valido para todo elemento x, então todo elemento de A está em B^c. Ou seja,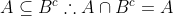 

Só isso  Lembre-se que diagrama de Venn só serve para termos uma noção, e não é uma prova concreta.

Qualquer dúvida, só perguntar

Giiovanna

Parece-me que, na primeira linha faltou algo:

Vamos supor que  A ∩ B^c = A  Então, isso significa que A ⊂ B^c ou B^c ⊂ A

O que você acha?

Tem total razão, Elcio. Obrigada

Obrigado