Números primos
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Números primos
por gustavolz 20/4/2013, 5:25 pm
Seja N = (2^n) x p, onde n é um número natural qualquer e p é um número primo. Se o número N é igual à soma de todos os seus divisores próprios, então p é igual a:
a) 2^(n-1) - 1
b) 2^(n-1)
c) 2^(n+1) - 1
d) 2^(n+2) - 1
e)2^n -1
a) 2^(n-1) - 1
b) 2^(n-1)
c) 2^(n+1) - 1
d) 2^(n+2) - 1
e)2^n -1
- Spoiler:
- c
gustavolz- Jedi
- Mensagens : 285
Data de inscrição : 22/02/2012
Idade : 28
Localização : Brasil
Re: Números primos
por jrhwk 20/4/2013, 8:58 pm
Fatorando o número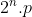 
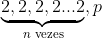
Encontrando seus divisores:
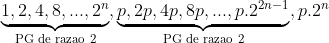
Devemos somar todos os divisores próprios do número, que são todos os seus divisores, sem contar ele mesmo. Temos duas PGs, vamos calcular a soma de cada uma e depois somar os resultados, dando a soma dos divisores próprios.
Primeira PG:
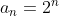
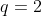
Vamos chamar o número de termos (geralmente chamado n, variável já utilizada aqui) de k.
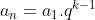
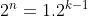
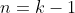
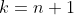
Soma da primeira PG
}{q-1})
}-1)}{2-1})
}-1})
Segunda PG:
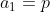
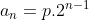
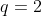
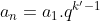
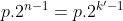
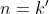
Soma da segunda PG
}{q-1})
}{2-1})
})
Basta agora somar os resultados e igualar a N, que é igual a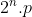
}-1 + p.(2^n-1) =2^n.p)
}-1 =2^n.p-p.(2^n-1))
}-1 =p(2^n-2^n+1))
}-1}})
Acho que existem jeitos mais rápidos de resolver, mas esse é o mais simples.
Encontrando seus divisores:
Devemos somar todos os divisores próprios do número, que são todos os seus divisores, sem contar ele mesmo. Temos duas PGs, vamos calcular a soma de cada uma e depois somar os resultados, dando a soma dos divisores próprios.
Primeira PG:
Vamos chamar o número de termos (geralmente chamado n, variável já utilizada aqui) de k.
Soma da primeira PG
Segunda PG:
Soma da segunda PG
Basta agora somar os resultados e igualar a N, que é igual a
Acho que existem jeitos mais rápidos de resolver, mas esse é o mais simples.
jrhwk- Iniciante
- Mensagens : 25
Data de inscrição : 20/03/2013
Idade : 29
Localização : br
Tópicos semelhantes» Qual a proporção entre números primos e não primos?
» Números Primos
» Números primos
» números primos
» Números Primos
» Números Primos
» Números primos
» números primos
» Números Primos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
