Partições

In how many ways can n students be partitioned into two teams containing at least one student?

Resp: 2^(n-1) -1

A resposta deriva daqui?



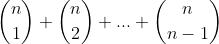
Ou analogamente pelo Binômio de Newton:

-1

Se alguém puder explicar melhor, agradeço

Olá:
Essa talvez seja a forma mais simples de perceber.Podia-se, no entanto, seguir outro raciocínio:
Designemos as duas equipas por A e B. O 1º estudante podia ficar na A ou na B--2 hipóteses;o 2º estudante podia igualmente ficar na A ou na B--2 hipóteses, e assim sucessivamente. Então para n estudantes haveria 2*2*...2=2^n hipóteses. Mas como as duas equipas são indistinguíveis ( o que nos interessa é dividir os alunos em 2 grupos), isso origina uma duplicação de casos (por exemplo, se n=5, AABBB seria o mesmo que BBAAA, tal como AAAAA srá o mesmo que BBBBB). Então há que dividir por 2: 2^n/2=2^(n-1). Mas há ainda um problema: os n alunos podiam ficar todos no mesmo grupo (AAAAA). Daí termos de subtrair 1 para respeitar a condição de as duas equipas contenham pelo menos um elemento cada, pelo que o resultado final será 2^(n-1)-1.Espero que tenha entendido.
Um abraço.

Perfeito Parofi, obrigada.

O meu problema era com o n-1. Entendi o porque de dividir por 2, ficou bem claro