Revisão de Funções
Página 1 de 1
 Revisão de Funções
Revisão de Funções
Curso elementar de cálculo – Revisão de Funções
- Introdução:
- O cálculo é sem dúvida uma das maiores descobertas da matemática. Seu estudo e aplicações resultaram em resoluções de problemas até então ditos impossíveis, proporcionou resoluções muito mais elegantes para questões já resolvidas, além de levar a mente humana a um novo patamar de raciocínio e perspectiva. Sua descoberta (digo assim porque creio que na matemática não inventamo s nada, apenas descobrimos algo já existente e premeditado) é creditada a Isaac Newton e Gottfried Leibniz , sendo este último o principal responsável pela notação até hoje usada.
Antes da explanação do cálculo propriamente dito, devemos dominar o estudo das funções, por isso façamos no tópico 1 a revisão de tal assunto.
- Tópico 1 – Revisão de funções:
- É extremamente necessário que quem estude este tópico já tenha estudado tudo sobre funções, de modo que sirva realmente apenas como revisão.
Em uma abordagem direta e axiomática, podemos definir uma função como uma relação entre conjuntos, uma lei na qual cada valor de x é correspondido ou não por outro valor de y.
A partir daqui iremos definir funções do tipo
Os valores que x assume são o conjunto domínio, os valores que y pode assumir são o conjunto contradomínio, e os valores que y de fato assume são o conjunto imagem. Nota que o conjunto imagem é um subconjunto do conjunto contradomínio.
Definições Gerais
Podemos definir a princípio 3 tipos de funções:
-Função injetora (injetiva): é aquela em que cada elemento da imagem está associado a apenas um elemento do domínio.
-Função sobrejetora (sobrejetiva): é aquela na qual o conjunto imagem é igual ao conjunto contradomínio. Em outras palavras, a função é sobrejetora quando todo elemento da imagem é imagem de pelo menos um elemento do domínio.
-Função bijetora: é aquela que é simultaneamente injetora e sobrejetora.
É perceptível que a função só admitirá inversa caso seja bijetora.
Outro tipo de definição (paridade de uma função):
-Função par: é aquela em que f(k) = f(-k)
-Função impar: é aquela em que f(k) = -f(-k)
- Principais funções:
Função afim
Função polinomial do primeiro grau, ou até mesmo função linear. É toda função na forma, onde a é o chamado coeficiente angular, que é a tangente do ângulo de inclinação da reta medido no sentido trigonométrico e b é o coeficiente linear, que é onde a função intercepta o eixo das ordenadas. Seu gráfico é uma reta oblíqua:
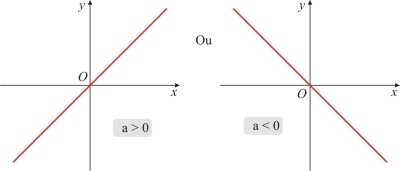
Função quadrática
Função polinomial do segundo grau. É toda função na forma. Seu gráfico é uma parábola, cuja concavidade varia conforme o sinal do coeficiente do termo de grau 2, no caso o a.
.jpg)
Seu ponto de mínimo é chamado vértice e é um ponto de coordenadas. No tópico de derivadas será feita uma análise deste ponto sob outra perspectiva.
Função composta
A função composta é aquela que nasce da junção de outras duas funções. Por exemplo:
Não há um gráfico definido, uma vez que se variam as funções envolvidas.
Função modular
É aquela que associa cada elemento x a seu módulo |x|. Tem-se por definição:
Considera-se o módulo como o valor absoluto do número, ou seja, por exemplo: |+5| = |-5| = 5
Operações básicas (exemplo de aplicação):
Para k > 0
O gráfico da Função modular será o gráfico da função padrão, só que com a parte negativa refletida, uma vez que por definição a função modular agrega apenas valores positivos.
Sendo:
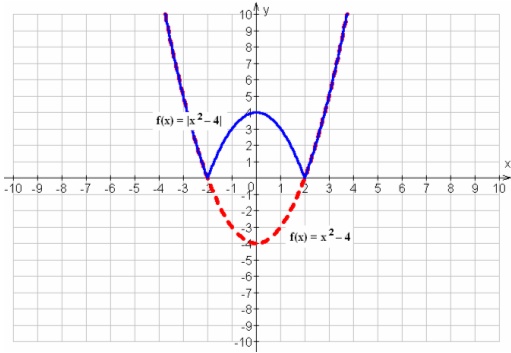
Função exponencial
A função exponencial é aquela que obedece à seguinte lei de formação:
Seu gráfico apresenta o eixo X como assíntota:.jpg)
Dica: rever propriedades de potências
Função logarítmica
A função logarítmica é aquela que obedece à seguinte lei de formação:
Seu gráfico apresenta o eixo Y como assíntota, e é crescente para a > 1 e decrescente para 0 < a < 1, conforme as tradicionais propriedades exponenciais:
Crescente:.jpg)
Decrescente:.jpg)
Dica: rever propriedades de logaritmos.
Há também as funções trigonométricas, mas como seu uso é frequente e importante para limites, derivadas e integrais, um tópico especial para elas será providenciado.
- Questões de aplicação:
1) A função f(x) = x² + bx + c, definida para qualquer valor real x, é nula para x = r ou x = 3r. Determine r sabendo que o valor mínimo de f(x) é -9.
2) Determine a soma das raízes da equação.
3) Seja f(x) uma função cujo domínio é o conjunto dos números inteiros e que associa a cada inteiro ímpar o valor zero e a todo inteiro par o triplo do seu valor. Calcule.
4) Uma substância radioativa está em processo de desintegração, de modo que no instante t a quantidade não desintegrada obedece à lei, onde A(0) indica a quantidade da substância no instante t = 0. Calcule o tempo necessário para que metade da substância se desintegre.
5) Uma sequênciaé definida por:
para
.
Sendoe
, calcule
.
Gabarito:
1) r = 3 ou r = - 3
2) 10/3
3) 3k(k – 1)
4)
5) 5
Última edição por JoaoGabriel em Dom 03 Fev 2013, 11:32, editado 1 vez(es)

JoaoGabriel- Monitor

- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
acpaz, Fibonacci13, Sublimacao188 e labash gostam desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Revisão e Fixação
» revisão ens. fundamental
» Revisão dos estudos
» Revisão de redação
» Revisão de Trigonometria
» revisão ens. fundamental
» Revisão dos estudos
» Revisão de redação
» Revisão de Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












