Geometria espacial - prisma
4 participantes
Página 1 de 1
 Geometria espacial - prisma
Geometria espacial - prisma
(Unesp) Uma caixa d'água com a forma de um paralelepípedo reto de 1m x 1m de base e (√3/2)m de altura, está sobre uma laje horizontal com água até a altura h. Suponhamos que a caixa fosse erguida lateralmente, apoiada sobre uma das arestas da base (que é mantida fixa), sem agitar a água. Assim sendo, a água começaria a transbordar exatamente quando o ângulo da base da caixa com a laje medisse 30º. Calcular a altura h.
Se possível, gostaria do desenho, porque não estou conseguindo visualizá-lo.
- Spoiler:
- h = (√3)/3 metros
Se possível, gostaria do desenho, porque não estou conseguindo visualizá-lo.

Bá Poli- Grupo
Velhos amigos do Fórum
- Mensagens : 478
Data de inscrição : 20/06/2012
Idade : 28
Localização : São Paulo - SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
Bá Poli
Vou dar a dica do desenho:
0) A caixa dágua tem base inferior ABCD e superior EFGH
1) Desenhe uma vista frontal da caixa dágua: é um retângulo de base AB = 1 e altura AE = √3/2
2) Na posição normal, com a base assentada na laje horrizontal o volume de água é dado por:
V = Sb*h ----> V = 1.1.h ----> V = h m³
3) Desenhe agora uma reta horizontal (a laje). Trace a partir de um ponto A uma reta inclinada AE de 30º com a laje e comprimento AE = √3/2. Complete o retângulo ABFE onde AB é uma das arestas visíveis da base, BF = AE e EF a aresta superior (visível) da caixa
Complete a parte de trás do prisma, colocando os vértices C, D, G, H e desenhe as arestas faltantes.
5) Escolha um ponto P qualquer de AB. A reta PE representa a superfície da água que começa a vazar e que AÊP = 30º (opostos pelo vértice):
tgAÊP = AP/AE ----> √3/3 = AP/(√3/2 ----> AP = 1/2
5) Note agora que a água ocupa um prisma triangular de base APE e altura AD = 1
V = S'*AD ----> V = (AE*AP/2)*AD ----> V = [(√3/2)*(1/2)/2]*1 ----> V = √3/8 m³
Comparando os dois volumes ----> h = √3/8
Note que existe uma diferença quanto ao seu gabarito: 8 ao invés de 3 no denominador
Vou dar a dica do desenho:
0) A caixa dágua tem base inferior ABCD e superior EFGH
1) Desenhe uma vista frontal da caixa dágua: é um retângulo de base AB = 1 e altura AE = √3/2
2) Na posição normal, com a base assentada na laje horrizontal o volume de água é dado por:
V = Sb*h ----> V = 1.1.h ----> V = h m³
3) Desenhe agora uma reta horizontal (a laje). Trace a partir de um ponto A uma reta inclinada AE de 30º com a laje e comprimento AE = √3/2. Complete o retângulo ABFE onde AB é uma das arestas visíveis da base, BF = AE e EF a aresta superior (visível) da caixa
Complete a parte de trás do prisma, colocando os vértices C, D, G, H e desenhe as arestas faltantes.
5) Escolha um ponto P qualquer de AB. A reta PE representa a superfície da água que começa a vazar e que AÊP = 30º (opostos pelo vértice):
tgAÊP = AP/AE ----> √3/3 = AP/(√3/2 ----> AP = 1/2
5) Note agora que a água ocupa um prisma triangular de base APE e altura AD = 1
V = S'*AD ----> V = (AE*AP/2)*AD ----> V = [(√3/2)*(1/2)/2]*1 ----> V = √3/8 m³
Comparando os dois volumes ----> h = √3/8
Note que existe uma diferença quanto ao seu gabarito: 8 ao invés de 3 no denominador

Elcioschin- Grande Mestre

- Mensagens : 73168
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
Consegui fazer o desenho do paralelepípedo inclinado, porém fiz a conta indicada pelo mestre Euclides e a altura deu diferente (bateu com a do gabarito):
[(√3 - 2h)/2] * 2 = √3/3
3√3 - 6h = √3
6h = 2√3
h = √3/3
[(√3 - 2h)/2] * 2 = √3/3
3√3 - 6h = √3
6h = 2√3
h = √3/3

Bá Poli- Grupo
Velhos amigos do Fórum
- Mensagens : 478
Data de inscrição : 20/06/2012
Idade : 28
Localização : São Paulo - SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
Meu desenho ficou assim:
(não consegui ir ao passo 5)
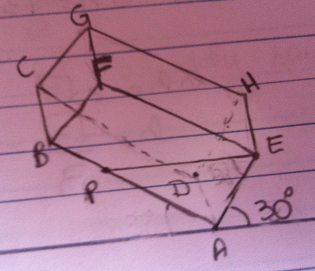
(não consegui ir ao passo 5)


Bá Poli- Grupo
Velhos amigos do Fórum
- Mensagens : 478
Data de inscrição : 20/06/2012
Idade : 28
Localização : São Paulo - SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
Você, em verdade, não precisa do paralelepípedo todo. Basta uma face:


____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
Entendi perfeitamente agora!!!  Muito obrigada mestres, Euclides e Elcio.
Muito obrigada mestres, Euclides e Elcio.

Bá Poli- Grupo
Velhos amigos do Fórum
- Mensagens : 478
Data de inscrição : 20/06/2012
Idade : 28
Localização : São Paulo - SP
 Re: Geometria espacial - prisma
Re: Geometria espacial - prisma
Estou postando meio atrasado as figuras , na qual a figura 1 representa o paralelepípedo no plano normal sem inclinação. Já a figura 2 representa o paralelepípedo com inclinação de 30°.
Mais uma vez, me desculpem pelo desenho, não aprendi a usar direito as ferramentas ainda, mas vamos lá.


Resolução :
No triângulo ABC, (figura 2) AB = 1 m e θ = 30°.
Logo aplicamos : tan 30° = BC / AB
Onde BC = √3/3.
A parte da caixa sem água tem volume (V ) :
V = 1/2 . a . b . c
V = 1/2 . √3/3 . 1 . 1
V = √3/6
O volume da água (V água ) :
V(água) = a . b . c
V(água) = 1 . 1 . h
V(água) = h
O volume da caixa ( V caixa ) :
V (caixa) = a . b . c
V (caixa) = 1 . 1 . √3/2
V (caixa) = √3/2
Como :
V água + V = V (caixa )
h + √3/6 = √3/2
h = √3/2 - √3/6
h =( 6√3 - 2√3 ) / 12
h = 4√3 / 12 ( simplificamos por 4)
h = √3/3 m ( resposta)
Mais uma vez, me desculpem pelo desenho, não aprendi a usar direito as ferramentas ainda, mas vamos lá.


Resolução :
No triângulo ABC, (figura 2) AB = 1 m e θ = 30°.
Logo aplicamos : tan 30° = BC / AB
Onde BC = √3/3.
A parte da caixa sem água tem volume (V ) :
V = 1/2 . a . b . c
V = 1/2 . √3/3 . 1 . 1
V = √3/6
O volume da água (V água ) :
V(água) = a . b . c
V(água) = 1 . 1 . h
V(água) = h
O volume da caixa ( V caixa ) :
V (caixa) = a . b . c
V (caixa) = 1 . 1 . √3/2
V (caixa) = √3/2
Como :
V água + V = V (caixa )
h + √3/6 = √3/2
h = √3/2 - √3/6
h =( 6√3 - 2√3 ) / 12
h = 4√3 / 12 ( simplificamos por 4)
h = √3/3 m ( resposta)
Última edição por Ademir Sott em Sex 03 maio 2013, 22:43, editado 1 vez(es)
Ademir Sott- Jedi

- Mensagens : 270
Data de inscrição : 14/12/2012
Idade : 55
Localização : Pimenta Bueno, RO, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Geometria Espacial - Prisma
» Geometria Espacial: Prisma
» GEOMETRIA ESPACIAL PRISMA
» Geometria Espacial- Prisma 2
» Geometria espacial (prisma)
» Geometria Espacial: Prisma
» GEOMETRIA ESPACIAL PRISMA
» Geometria Espacial- Prisma 2
» Geometria espacial (prisma)
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













