Número complexos/Soma de vetores
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Número complexos/Soma de vetores
por soniky Seg 03 Dez 2012, 03:13
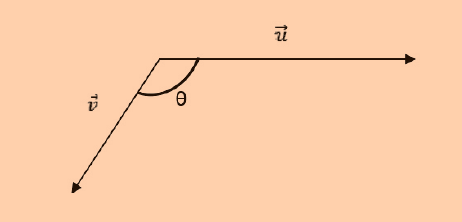
Os vetores u e v, representados na figura a seguir, têm módulos, respectivamente,
iguais a 8 e 4, e o ângulo θ mede 120º. Qual é o módulo do vetor u - v?
Gabarito: 4√3 (quatro raíz de três).
___________________________________________________________
Meu raciocínio:
Transformei cada vetor em um número complexo:
u = 8 +0i
v = -2-2√3i
Então fiz u-v = (8+0i) - (-2-2√3i) = 10+2√3i
Calculando o módulo desse número: x² = 10² + (2√3)²
x = 4√7
O que estou fazendo de errado?
iguais a 8 e 4, e o ângulo θ mede 120º. Qual é o módulo do vetor u - v?
Gabarito: 4√3 (quatro raíz de três).
___________________________________________________________
Meu raciocínio:
Transformei cada vetor em um número complexo:
u = 8 +0i
v = -2-2√3i
Então fiz u-v = (8+0i) - (-2-2√3i) = 10+2√3i
Calculando o módulo desse número: x² = 10² + (2√3)²
x = 4√7
O que estou fazendo de errado?
soniky- Recebeu o sabre de luz
- Mensagens : 157
Data de inscrição : 18/08/2011
Idade : 34
Localização : Guará - Distrito Federal (BR)
Re: Número complexos/Soma de vetores
por aprentice Seg 03 Dez 2012, 04:18
Absolutamente nada, o gabarito está incorreto.
Outra solução:
u - v = u + (-v)
Note que o angulo entre u e -v é de 60 graus.
Então:
|u + (-v)| = sqrt(|u|² + |v|² + 2|u||v|cos(60)) = sqrt(64 + 16 + 32) = 4sqrt(7)
Outra solução:
u - v = u + (-v)
Note que o angulo entre u e -v é de 60 graus.
Então:
|u + (-v)| = sqrt(|u|² + |v|² + 2|u||v|cos(60)) = sqrt(64 + 16 + 32) = 4sqrt(7)
aprentice- Jedi
- Mensagens : 355
Data de inscrição : 28/09/2012
Idade : 30
Localização : Goiânia - Goiás - BR
Tópicos semelhantes» Soma de numero complexos com módulo
» Soma de vetores
» Soma de vetores
» Soma de Vetores
» Soma de vetores
» Soma de vetores
» Soma de vetores
» Soma de Vetores
» Soma de vetores
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
