Teorema de Cauchy (Matrizes)

por **Robson Jr.** Dom 16 Set - 19:00

Neste tópico provarei um resultado auxiliar a ser usado na demonstração do "Método da Adjunta para Cálculo de Inversas".

Haverá duas seções:

● Demonstração para matrizes de ordem 3, para que o raciocínio desenvolvido fique claro;
● Demonstração para matrizes de ordem qualquer.

Adiante:

Teorema de Cauchy
É nula a soma dos produtos dos elementos de uma fila pelos cofatores dos elementos correspondentes noutra fila paralela.

Demonstração para matrizes 3x3:

Considere uma matriz de elementos genéricos:

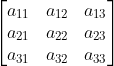
$\begin{bmatrix} a_{11} &a_{12} &a_{13} \\ a_{21} &a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \end{bmatrix}$

Partindo, sem perda de generalidade, da Linha 1 e usando como fila paralela a Linha 2, nossa conjetura torna-se:

$\small a_{11}.(-1)^{2+1} \begin{vmatrix} a_{12} &a_{13} \\ a_{32} &a_{33} \end{vmatrix}+ a_{22}.(-1)^{2+2} \begin{vmatrix} a_{11} &a_{13} \\ a_{31} &a_{33} \end{vmatrix}+ a_{13}.(-1)^{2+3} \begin{vmatrix} a_{11} &a_{12} \\ a_{31} &a_{32} \end{vmatrix}=0$

Mas o membro esquerdo pode ser visto como a aplicação da Regra de Laplace na linha 2 do seguinte determinante:

$\begin{vmatrix} a_{11} &a_{12} &a_{13} \\ a_{11} &a_{12} &a_{13} \\ a_{31} &a_{32} &a_{33} \end{vmatrix}$

Como um determinante com duas filas paralelas iguais é nulo, o teorema se confirma para ordem 3. CqD

Demonstração para matrizes nxn:

Seja uma matriz qualquer:

$\begin{bmatrix} a_{11} &a_{12} &a_{13} &... &a_{1n} \\ a_{21} &a_{22} &a_{23} &... &a_{2n} \\ a_{31} &a_{32} &a_{33} &... &a_{3n} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n2} &a_{n3} &... &a_{nn} \end{bmatrix}$

Partindo, sem perda de generalidade, da Linha 1 e usando como fila paralela a Linha 2, a conjetura pode ser escrita como:

$\small a_{11}.(-1)^{2+1} \begin{vmatrix} a_{12} &a_{13} &... &a_{1n} \\ a_{32} &a_{33} &... &a_{3n} \\ \vdots &\vdots &\ddots &\vdots \\ a_{n2} &a_{n3} &... &a_{nn} \end{vmatrix}+ a_{12}.(-1)^{2+2} \begin{vmatrix} a_{11} &a_{13} &... &a_{1n} \\ a_{31} &a_{33} &... &a_{3n} \\ \vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n3} &... &a_{nn} \end{vmatrix}+...+ a_{1n}.(-1)^{2+n} \begin{vmatrix} a_{11} &a_{12} &... &a_{1(n-1)} \\ a_{31} &a_{32} &... &a_{3(n-1)} \\ \vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n2} &... &a_{n(n-1)} \end{vmatrix}\\=0$

Mas o membro esquerdo pode ser visto como a aplicação da Regra de Laplace na linha 2 do seguinte determinante:

$\begin{bmatrix} a_{11} &a_{12} &a_{13} &... &a_{1n} \\ a_{11} &a_{12} &a_{13} &... &a_{1n} \\ a_{31} &a_{32} &a_{33} &... &a_{3n} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n2} &a_{n3} &... &a_{nn} \end{bmatrix}$

Como um determinante com duas filas paralelas iguais é nulo, o teorema se confirma para qualquer ordem. CqD

O tópico abordando o método citado será criado em breve.