Circunferência

por mateus90 Sáb 15 Set 2012, 18:12

Umas das retas paralelas à reta r: 3x - 4y = 0 e tangente à circunferência de equação (x - 5)² + (y - 1)² = 4 tem por equação:

a)3x - 4y - 20 = 0
b)3x - 4y - 21 = 0
c)3x - 4y - 22 = 0
d)3x - 4y - 23 = 0
e)3x - 4y - 24 = 0

por **Elcioschin** Sáb 15 Set 2012, 18:30

3x +4y = 0 ----> y = (-3/4)*x ----> m = - 3/4

Faça um desenho em escala: loque a reta acima e a circunferência com centro C(5 1) e raio R = 2

Note que são duas retas paralelas tangentes à circunferência. A equação geral delas é y = (-3/4))*x + k

Substitua y na equação da circunferência: você obterá uma equação do 2º grau na varável x ----> ax² + bx + c = 0

Calcule o discrimnante ∆= b² - 4ac ----> Para a reta ser tangente ∆= 0

Faça∆ = 0 e calcule os valores de k que atendem e volte na equação da reta

Pronto

por William Carlos Sáb 15 Set 2012, 18:56

Olá!

Gostaria que verifica-se a pergunta,pois creio que a reta r tenha como equação 3x-4y=0 e não 3x+4y=0,Até.

por William Carlos Sáb 15 Set 2012, 19:11

Segue a solução para r:3x-4y=0

$Circunferência Gif$

m=3/4

Como são retas paralelas,possuem o mesmo coeficiente angular,portanto a equação da reta procurada sera da forma.

$Circunferência Gif$

Como o raio vale 2, e esta reta é tangente à circunferência,temos que a distancia entre o centro e a reta sera 2.

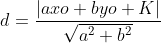
$Circunferência Gif$

Sendo:
d=2
a=3,b=4,k
xo=5,yo=1

Substituimos e resolvemos para k.

$2=\frac{|(3*5)+(-4*1)+k|}{\sqrt{3^{2}+4^{2}}}\rightarrow2=\frac{|11+k|}{5} \rightarrow 10=|11+k|$

Resolvendo temos que k=-1 ou k=-21

-4y+3x-21=0------>3x-4y-21=0

Perceba que eu cheguei no resultado fazendo r:3x-4y=0, e não 3x+4y=0 como postou.

Espero ter ajudado.