IME - Polinômios

(IME) Encontre o polinômio tal que e é divisível por 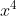, onde é um polinômio de 6º grau.

Primeiramente, gostaria de saber como resolver essa questão.
Minha outra pergunta é: é possível fazê-la apenas com assunto do ensino médio?
E por último: se a informação "...onde é um polinômio de 6º grau" fosse omitida, ainda assim seria possível resolver a questão?

Desculpe se foram muitas as perguntas, mas essa questão caiu em uma prova minha de matemática (claro xP) e não consegui resolvê-la, mas na minha prova faltou a informação a respeito do grau de Q(x). Se puderem me ajudar, agradeço desde já!

Vamos ver isso daí...

Q(x) + 1 = (x - 1)³ * P(x)
Se Q(x) é um polinômio do sexto grau, isso significa que P(x) deve ter grau 3. Dessa maneira, poderemos multiplicar o x³ daquela parte ali que está ao cubo com um x³ do polinômio e dará o x^6 que existe do outro lado da equação. Para igualar então, precisamos que P(x) tenha grau três. Vou tentar explanar mais para ver se fica mais compreensível.
Q(x) + 1 = (x - 1)³ * P(x)
Q(x) + 1 = (x³ - 3x²+ 3x - 1) * P(x)
Q(x) = (x³ - 3x² + 3x - 1) * P(x) - 1
E agora? Ficou melhor? Pois bem, sabemos que Q(x) + 2 é divisível por x^4. Isso quer dizer que, por ser divisível por x^4, você tem que todos os coeficientes tem grau quatro para cima, caso contrário, você não teria esse tipo de divisão com resto zero. Ou seja...
Q(x) + 2 = (x³ - 3x² + 3x - 1) * P(x) + 1
E que o outro lado da equação também é divisível por 4. Como sabemos que P(x) é do terceiro grau, vou usar de um artifício que no começo parece complicado, mas depois facilita.
(x³ - 3x² + 3x - 1) * (ax³ + bx² + cx + d) + 1 = ax^6 + (b - 3a)x^5 + (3a - 3b + c)x^4 + (3b - a - 3c + d)x³ + (3c - 3d - b)x² + (3d - c)x - d + 1
Lembrando que, na equação Q(x) nós só temos termos de grau quatro até grau seis, ou seja, podemos igualar os outros coeficientes a zero e determinar seus valores a partir disso.
- d + 1 = 0 -> - d = - 1 -> d = 1
3 - c = 0 -> - c = - 3 -> c = 3
9 - 3 - b = 0 -> 6 - b = 0 -> - b = - 6 -> b = 6
18 - a - 9 + 1 = 0 -> - a + 10 = 0 -> - a = - 10 -> a = 10

Então...
3a - 3b + c = 30 - 18 + 3 = 15
b - 3a = 6 - 30 = - 14
a = 10

Logo, Q(x) = 10x^6 - 14x^5 + 15x^4.

Espero ter ajudado. ^_^

Ok, então peo que vi só seria possível resolver essa questão sabendo que o polinômio Q(x) é de grau 6, certo? Ah, e obrigado Agente Esteves

Sim, só é possível com essa informação mesmo. =]