Funções Contínuas
4 participantes
Página 1 de 1
Funções Contínuas
por mirlane Sáb 14 Abr 2012, 13:45
Boa tarde!
Aguém pode me ajudar!
Se a> 0. Determine o valor de C para que a função f : [ 0, + infinito] =\frac{\sqrt{x}- \sqrt{a}}{x - a})
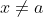se 
e  = c)
, seja contínua em a.
Abraços Mirlane
Aguém pode me ajudar!
Se a> 0. Determine o valor de C para que a função f : [ 0, + infinito]
Abraços Mirlane
mirlane- Recebeu o sabre de luz
- Mensagens : 144
Data de inscrição : 13/04/2012
Idade : 35
Localização : Barão de Cocais - MG - Br
Re: Funções Contínuas
por Elcioschin Sáb 14 Abr 2012, 15:26
.......... \/x - \/a ...............\/x - \/a ...................... 1
f(x) = ------------ = ---------------------------- = -------------
............ x - a ......... (\/x - \/a)*(\/x + \/a) ......\/x + \/a
................. 1 ............... 1
f(a) = ------------- = ----------
........... \/a + \/a ...... 2*\/a
.......... 1
c = --------
....... 2*\/a
f(x) = ------------ = ---------------------------- = -------------
............ x - a ......... (\/x - \/a)*(\/x + \/a) ......\/x + \/a
................. 1 ............... 1
f(a) = ------------- = ----------
........... \/a + \/a ...... 2*\/a
.......... 1
c = --------
....... 2*\/a
Elcioschin- Grande Mestre
- Mensagens : 73181
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Funções Contínuas
por mirlane Sáb 14 Abr 2012, 15:50
Olá Elcio vc Fez a multiplicação pelo conjugado?
mirlane- Recebeu o sabre de luz
- Mensagens : 144
Data de inscrição : 13/04/2012
Idade : 35
Localização : Barão de Cocais - MG - Br
Re: Funções Contínuas
por rihan Sáb 14 Abr 2012, 15:52
É só calcular o limite de f(x), quando x ---> a
Vai dar uma indeterminação do tipo 0/0.
L'Hôpital:
lim (f(x)) = lim ( g(x)/h(x) ) = lim ( g'(x)/h'(x) )=
(1/2)x^(-1/2)/1 = (1/2)a^(-1/2) = (1/2)/√(a) =√(a)/2a
Vai dar uma indeterminação do tipo 0/0.
L'Hôpital:
lim (f(x)) = lim ( g(x)/h(x) ) = lim ( g'(x)/h'(x) )=
(1/2)x^(-1/2)/1 = (1/2)a^(-1/2) = (1/2)/√(a) =√(a)/2a
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Re: Funções Contínuas
por rihan Sáb 14 Abr 2012, 15:56
mirlane escreveu:Olá Elcio vc Fez a multiplicação pelo conjugado?
Não, mestre Elcio percebeu que :
(V(x) - V(a))/(x-a) = 1/(V(x) + V(a) )
E demonstrou pra você o porquê.
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Re: Funções Contínuas
por Medeiros Sáb 14 Abr 2012, 16:22
mirlane, a inteligente jogada do Elcioschin foi essa:
x=(√x)² e a=(√a)²
x - a = (√x)² - (√a)² = (√x - √a)*(√x + √a)
e fez isso para poder aplicar, no denominador, o produto notável da diferença dos quadrados e poder cancelar com o numerador, tirando a indeterminação.
x=(√x)² e a=(√a)²
x - a = (√x)² - (√a)² = (√x - √a)*(√x + √a)
e fez isso para poder aplicar, no denominador, o produto notável da diferença dos quadrados e poder cancelar com o numerador, tirando a indeterminação.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
rihan- Estrela Dourada
- Mensagens : 5049
Data de inscrição : 22/08/2011
Idade : 69
Localização : Rio de Janeiro, RJ, Itabuna-Ilhéus, BA, Brasil
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
