Financeira - (valor atual)

Relembrando a primeira mensagem :

Olá, estou estudando matemática financeira e estou com um problema:

Uma empresa emprestou R$8.000,00 (F), e dois meses antes do vencimento resgatou-se o título. Determine o Valor Atual (P), sabendo que a taxa de desconto é 3% a.m..

o exemplo possuia a segunte solução:


O meu problema está ai, "Resgatar o título é o mesmo que quitar a dívida?"
Eu empresto dinheiro dinheiro com juros, e a pessoa antes de terminar o praso me devolve o dinheiro e me paga menos do que eu emprestei? É isso mesmo? Como a empresa lucra com os empréstimos? Se for assim, pedirei mil reais emprestado e uma semana depois vou no banco um uma nota de dois reais e pago a minha dívida. Acho que não entendi alguma coisa!
Outra coisinha: "Como devo saber que se trata, com nesse exemplo, de Desconto Racional Composto, ou qualquer outro tipo de desconto?"
era só isso tudo rs, agradeço desde já a paciência de ter lido até aqui e não ter desistido...
até +
Wanafunzi (Lucas Araújo)

ERA UMA VEZ ZÉ, O ENROLADO.
_____________________________

Continuação - IV PARTE
_______________________________________________

Uma BOA imagem vale mais do que... muitas coisas !

______________________________________________


P3: Dados V₀ , V_n , 0, f_p e p . Pede-se n = ?

a) Um pai quer dar um carro zero a seu filho recém-nascido quando este entrar na faculdade. Ele quer dar um carro que valha atualmente algo em torno de R$ 40 000,00. Ele então abriu hoje mesmo uma caderneta de poupança com depósito inicial de R$ 1 000,00 e, internamente, jurou pra si mesmo que jamais mexeria nela até a data da surpresa !

(I) Considerando-se uma taxa média mensal de remuneração de 0,5% a.m. — além da correção monetária — e que seu filho deverá estar com 18 anos quando entrar no Ensino Superior, será que ele vai conseguir dar o presente na época certa ?

Dados:

V₀ = 1 000

V_n = 40 000

p = 1 m

j = 0,5% am = 5/100 = 0,005 am

f_m = 1 + j = 1 + 0,005 = 1,005

Δt = 18 a = 18 a .12 m/a = 216 m

Pede-se:

n= ?

Então:

V_n = V₀. f_pⁿ

V_n = V₀. f_mⁿ

V_n = V₀. f_mⁿ

f_mⁿ = V_n /V₀log( f_mⁿ ) = log( V_n / V₀ )

n.log( f_m ) = log( V_n / V₀ )

n = log( V_n / V₀ ) / log( f_m )

n = log( 40 000/1 000) / log (1,005 )

n = log( 40 ) / log (1,005 )

n ≈ 1,6021 / 0,0021661

n ≈ 740 m

Não conseguirá !!!

Caso não seja o saldo suficiente:

(II) Em quanto tempo após a data prometida haverá o saldo necessário ?

740 - 216 ≈ 524 m ≈ 44 anos após

b) Zé, O Enrolado, está hoje com um débito de R$ 2 000,00 :scratch: não quitado no seu cartão de crédito. Sabendo-se que a taxa média mensal de juro cobrada pelas administradoras de cartão de crédito é de 15% a.m., em quanto tempo sua dívida triplicará se ele "deixar rolar" e não amortecer qualquer valor ?

Dados:

V₀ = 2 000

V_n = 3V₀ = 6 000

p = 1 m

j = 15% am = 15/100 = 0,15 am

f_m = 1 + j = 1 + 0,15 = 1,15

Pede-se:

n= ?

Então:

V_n = V₀. f_pⁿ

V_n = V₀. f_mⁿ

V_n = V₀. f_mⁿ

f_mⁿ = V_n /V₀log( f_mⁿ ) = log( V_n / V₀ )

n.log( f_m ) = log( V_n / V₀ )

n = log( V_n / V₀ ) / log( f_m )

n = log( 6 000/2 000) / log (1,15 )

n = log( 3 ) / log (1,005 )

n ≈ 0,0477 / 0,0607

n ≈ 8 m !!!


P4: Dados V₀ , V_n , 0, ne p . Pede-se f_p = ? ( ou j_p )

a) Nosso amigo Zé quer comprar uma certa super-hiper TV-LED-HD-3D de 60" que custa à vista R$ 10 000,00 !!!

Na loja "A" tem uma "oferta sem juros" :face: : R$ 12 000,00 para ser pago 120 dias após a compra.

Na loja "B", outra "oferta" : R$ 11 000,00 para ser pago 60 dias após a compra.

Zé tem freqüentado assiduamente o PiR2 e não é mais uma anta :rendeer: e sabe que há juros nas "ofertas"... e

Pensou :scratch: , pensou :scratch: :scratch: e pensou... :scratch: :scratch: :scratch: e decidiu comprar na loja "B", achando que tinha a taxa de juro mensal menor.

(I) Quais as taxas efetivas mensais de cada loja ?

Dados Loja "A":

V₀ = 10 000

V_n = 12 000

Δt = 120 d = 120d/(30d/m) = 4 m

p = 1 m

n= 4

Pede-se:

j_m = ? (e f_m = ?)

Então:

V_n = V₀. f_pⁿ

V_n = V₀. f_mⁿ

V_n = V₀. f_mⁿ

f_mⁿ = V_n /V₀f_m= (V_n /V₀ )^1/n

f_m= ( 12 000 / 10 000 )^1/4

f_m= ( 1,2 )^1/4

f_m ≈ 1,046636

j_m ≈ 0,046636 ≈ 4,47% am para Loja "A"


Dados Loja "B":

V₀ = 10 000

V_n = 11 000

Δt = 60 d = 60d/(30d/m) = 2 m

p = 1 m

n= 2

Pede-se:

j_m = ? (e f_m = ?)

Então:

V_n = V₀. f_pⁿ

V_n = V₀. f_mⁿ

V_n = V₀. f_mⁿ

f_mⁿ = V_n /V₀f_m= (V_n /V₀ )^1/n

f_m= ( 11 000 / 10 000 )^1/2

f_m= ( 1,1 )^1/2

f_m ≈ 1,04881

j_m ≈ 0,04881 ≈ 4,88% a.m. para Loja "B"


(II) Zé estava correto ?

Não ! :evil: !

_______________________________________________________________________________________

RESUMÃO:

a) JURO (ou INTERESSE): J ≡ V_final - V_inicial

b) TAXA DE JURO: j ≡ J /V_{inicial =} ( V_final - V_inicial ) / V_inicial = V_final / V_inicial - 1

c) FATOR TEMPORAL: f_p ≡ 1 + j_p

d) NÚMERO DE PERÍODOS: n = Δt/p

e) VALOR NO TEMPO ("JUROS COMPOSTOS"): V_n = V₀. f_pⁿ

TERMINOLOGIA:

Valor Inicial: V₀ , Valor Atual (VA), Valor Presente (VP), Capital (C), Principal (P), ...

Valor Final: V_n , Valor Futuro (VF), Montante (M), ...

_____________________________________________________________________________________


Por enquanto estamos nas operações "pa-puf" ou "toma lá, dá cá". Temos dois movimentos somente:

1º: Uma entrada/saída de Valor.

2°: Uma saída/entrada de Valor.

Vamos agora visualizar estas movimentações através de um diagrama de fluxo ("Fluxo de Caixa", "Fluxo Financeiro"):

ERA UMA VEZ ZÉ, O ENROLADO.
_____________________________

Continuação - V PARTE
_______________________________________________

Uma BOA imagem vale mais do que... muitas coisas !

______________________________________________

Se Zé pegar emprestado do gentil financista, R$ 100,00 hoje, e devolver hoje mesmo, ele deverá devolver os mesmos exatos R$ 100,00.

Felizmente não há mais juros por minuto, nem por hora , sendo hoje, na quase totalidade dos países, o dia o menor período de tempo considerado.

Vamos mostrar isso de forma gráfica, o que facilita a compreensão e visualização dos problemas para a maioria das pessoas.

Vamos convencionar os sinais e usar a convenção normal de "positivo pra cima e pra direita, negativo pra baixo e pra esquerda".

A convenção contábil para valores é oposta, mas deixa isso pros contadores, para nós, meros mortais, entrou algo é positivo, saiu, é negativo !

O Eixo vertical é dos valores, o horizontal é do tempo.

Assim, o empréstimo de Zé fica representado graficamente por:



Neste caso:

V₀ = 100

V'₀ = -100

p = dia

Tataremos os valores como "vetores": pra cima positivo, pra baixo, negativo.

Então o SALDO, SOMA, SOMATÓRIO, MONTANTE ou BALANÇO seria, no  período "0":

S_n = V₀ + V'₀

S₀ = V₀ + (-V'₀ )

S₀ = 100 - 100

S₀ = 0

Mas Zé não tem jeito, sempre enrolado !

Precisou de R$ 100,00.

O gentil financista estipulou a taxa de juro em 1% ao dia.

Zé topou e  pegou no dia 1º de abril e só devolveu no dia 3, passados 2 dias.

Vamos calcular o saldo de Zé no dia 3 e saber quanto ele terá de pagar para saldar (quitar, resgatar) sua dívida.

O número do período  em que estamos interessados, onde está o nosso foco, é batizado de "DATA FOCAL".

Nesse caso nossa DATA FOCAL seria em 3 de abril, ou no período 2.

Vamos ver quanto vale os R$ 100,00 passados 2 dias sob a taxa de juro de 1% ao dia.

V₀ = 100

V₂ = ???

p = dia

j_d = 1 % = 0,01

f_d = 1 + j_d =  1,01

Vamos fazer o "fluxo de caixa" de Zé:



Para "andar" pra frente no tempo basta multiplicarmos pelo FATOR TEMPORAL a cada período.

Como foram 2 períodos, é mais sintético usarmos a notação de potência e multiplicarmos pelo fator elevado a 2.

V₂ = V₀ . f_d²

Nosso SALDO no período 2 ficaria:

S₂ = V₀ . f_d²

Obviamente que Zé zeraria o saldo pagando esse valor.

Mas, se quisermos algebricamente, poderíamos fazer assim:

Que valor V₂ zeraria o saldo ?

S₂ = V₀ . f_d² + V₂

S₂ = 0 ???

V₀ . f_d² + V2 = 0

V₂ =  - V₀ . f_d²

V₂ =  -100 . 1,01² = -100 .1,0201 = -102,01
Isto é, o negativo indica uma saída, um pagamento a ser efetuado por Zé ao gentil financista, no valor de R$ 102,01 .

Nosso fluxo fica assim:




Estamos quase chegando ao auge: A ÚNICA "FÓRMULA" DA MATEMÁTICA FINANCEIRA !!!

Enquanto isso, passados uns meses, eis que Zé, o Enrolado, pra variar, precisou de pedir um outro empréstimo ao gentil financista :twisted: ...

Pegou R$ 1 000,00 , à taxa de juro "módica", que o gentil financista só faz pra "amigos" :twisted: , de 1% ao dia !


Passados 3 dias ele recebeu um dinheiro e, preocupado com os juros, entregou R$ 200,00 ao gentil financista para amortecer a sua dívida, diminuir o seu saldo.

Passados mais 2 dias, fez outra amortização no valor de R$ 500,00.

Após mais 5 dias, recebeu uma bolada e resolveu quitar sua dívida, nas não sabia quanto era o seu saldo devedor ...

Vamos ajudar o Zé ...

Graficamente, fica assim:



Nossa "Data Focal" é o 10º período (dia).

Vamos equacionar:

f_d  = 1,01

V₀ = 1 000

V₃ = - 200

V₅ = - 500

V₁₀ = ??? para S₁₀ = 0 ???

S₁₀ = V₀ . f_d¹⁰ + V₃ . f_d⁷ + V₅ . f_d⁵  + V₁₀ = 0

1 000 . 1,01¹⁰- 200. 1,01⁷- 1,01⁵ + V₁₀ = 0

1 000 . 1,104622 - 200 . 1,072135 - 500 . 1,051010 + V₁₀ = 0

364,69 + V₁₀ = 0

V₁₀ = - 364,69

Prontinho Zé !!!

Vai ter que pagar ao GF somente R$ 364,69  !

Bem agora chegiu a hora !!!!

A ÚNICA "FÓRMULA" DA MATEMÁTICA FINANCEIRA !!! :bounce: :bounce: :joker: :geek:

________________________________________________________________________________________________

S_n = V₀ . f_pⁿ  + V₁ . f_p^n-1+  V₂ . f_p^n-2  .... +   V_n-1. f_p¹ + V_n
________________________________________________________________________________________________


Em notação mais sintética:



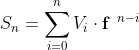
Continua >>> ... E Vamos Lá !!!
 

ERA UMA VEZ ZÉ, O ENROLADO.
_____________________________

Continuação - VI PARTE
_______________________________________________

Dinheiro não é tudo... mas é 100% !

Quase...

______________________________________________


Bem, finalmente temos nossa equação !!! A que resolve tudo nas finanças !!!

Vamos, para simplificar, chamar nosso "fator-máquina-do-tempo" f_p de somente x.

Nossa fantástica equação assim fica:

S_n = V₀.xⁿ + V₁.x^n-1 + V₂.x^n-2... V_n-1.x + V_n

Isso nada mais é que um poliômio de grau "n", né ?

Esse é um dos motivos importantes de se estudar os polinômios !

Agora que já sabemos a teoria TODA, vamos aplicá-la em diversos problemas e, paralelamente, aprendermos os termos usados na linguagem "financês", que, no fundo, é a única coisa complicada e chata.

P01 - Zé pega um empréstimo de R$ 1 000, 00 com taxa de 3% a.m. e prazo de 6 meses. Qual o valor que deverá ser pago ao final do prazo para zerar sua dívida ?

V₀ =1 000

p = m

Prazo = 6 meses

j = 3% a.m. = 0,03 am

x = 1,03

n = 6

S₆ = 0

V₆ = ?

Spoiler:

______________________________________

Fórmula:

V_n = -V₀ . xⁿ

______________________________________

P02 - Zé pegou um financiamento para a casa propria pelo "Sistema Price" *, a juros de 1% a.m. mais correção monetária para pagar os R$ 100 000,00 que pegou em 15 anos. Qual vai ser a prestação de Zé se não levarmos em conta a correção monetária ?

* Sistema Price: as prestações pagas (amortizações) são iguais.

V₀ =100 000

p = m

Prazo = 15 anos = 180 meses

j = 1% a.m. = 0,01 am

x = 1,01

n = 180

S₁₈₀ = 0

V_i = V ?

Spoiler:

____________________________________________________

Fórmula:

V = V₀ . xⁿ . ( x- 1 ) / ( xⁿ - 1)

____________________________________________________


Alguém notou alguma coisa diferente nas resoluções dos dois problemas ???? ????


P03 - Zé comprou um carro em 12 prestações mensais de R$ 4 000,00 . A taxa da financeira foi de 1,2% am . Qual o valor do carro ?

V₀ = ???

p = m

Prazo = 12 meses

j = 1,2% a.m. = 0,012 am

x = 1,012

n = 12

S₁₂ = 0

V_i = V = 4 000

Podemos proceder como de costume ou acelerar nossa resolução se soubermos a fórmula anterior de cor...

Vou usar a fórmula !!! :face: !!!

Spoiler: