( HARVARD ) Quociente de a/b ... !?

( HARVARD ) Os números a e b são inteiros. Sabe-se que , calcule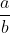

Pessoal tentei resolver esta questão, mas sempre me complico nas raízes.

Agradeço a quem puder ajudar.

Ps: Infelizmente não tenho o gabarito.

Obrigado.

Elevando-se à 2ª potência:

a² + b + 2a√b = 15 + √(216)

a² + b + 2a√b = 3.5 + √(2³.3³)

a² + b + 2a√b = 3.5 + 2.3√6

a² + b + 2a√b = 3² + 6 + 2.3√6

b = 6

a = 3

a/b = 3/6

a/b = 1/2

Impressionante amigo Rihan, obrigado mesmo.

Só não compreendi essa correspondência entre os membros ?


Mais uma vez obrigado.

É uma equação nos Inteiros, sendo b positivo não-nulo (é radicando e denominador).

Imagine então como um "polinômio-fantasma" sem os "x"...

Suponha:

ax² + bx = 3x² + 4x ---> a = 3 e b = 4

Saudações fantasmagóricas !

Gostei!

Eu não estava fazendo essa transformação de 3.5 para 3² + 3.2, tem que ter um bom olhar matemático para isso

Obrigado Rihan!

Só precisava:

... + 2a√b = ... + 2.3√6

Era o suficiente e necessário...

Coloquei o restante para "fortificar" !

Realmente o restante me ajudou muito também amigo rihan.

Obrigado de verdade.

outro modo por radical duplo

O método apresentado por christian é interessante pois demanda menos tempo.

Mas ganhar tempo é gastar espaço, mais uma coisa a decorar, a ocupar espaço no separador de orelhas...

Vamos analisá-lo:

Dado um "radical duplo":

√(m + √n)

Onde, obviamente, "n" não é quadrado perfeito, ou, em outras palavras, "√n" é irracional.

Transformá-lo numa soma de "radicais simples":

√a + √b

Equacionando-se, para se descobrir as incógnitas "a" e "b":

√(m + √n) = √a + √b

[√(m + √n)]² = [√a + √b]²

m + √n = a + b + 2√a√b

m + √n = a + b + 2√(ab)

Temos o "polinômio fantasma", isto é, partes racionais e partes irracionais.

Vamos igualá-las.

Racionais:

m = a + b

Irracionais:

√n = 2√(ab)

[√n]² = [2√(ab)]²

n = 4ab

Temos um sistema:

a + b = m

ab = n/4

Composto de soma e produto de duas incógnitas.

Vamos resolvê-lo.

Em vez de fazermos por substituição ( tipo "b = m - a" ) ou pela soma e produto na equação de 2º grau, vamos variar:


[a + b]² = [m]²

(4)ab = (4)n/4


a² + 2ab + b² = m²

4ab = n

Subtraindo-se:

a² - 2ab + b² = m² - n

(a - b)² = m² - n

Que implica na restrição: m² > n

a - b = ±√(m² - n)

Temos agora:

a + b = m

a - b = ±√(m² - n)

Chmando-se:

√(m² - n) ≡ c

Ficando:

a + b = m

a - b = ±c

Somando-se:

2a = m ± c

a = (m ± c)/2

Subtraindo-se:

2b = (m ∓ c)

b = (m ∓ c)/2

Simplificando, no caso de a > b :

Sendo pedido:

√(m + √n) = √a + √b

Calculamos:

c = √(m² - n)

E:

a = (m + c)/2

b = (m - c)/2

Na nossa questão:

c = √(15² - 216) = = √(225 - 216) = √9 = 3

a = (15+3)/2 = 9

b = (15-3)/2 = 6

Então:

√(15 + √216) = √9 + √6 = 3 + √6

Sendo o "a" e "b" da questão: a + √b

Temos:

a = 3

b = 6

a/b = 1/2

Saudações detalhadas !

E Vamos Lá !!! !!!