Construção de um gráfico de uma função do tipo seno
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 Construção de um gráfico de uma função do tipo seno
Construção de um gráfico de uma função do tipo seno
Determine o período e a imagem e faça o gráfico de um período completo das funções abaixo:
[latex]f:\mathbb{R}\rightarrow \mathbb{R} \; dada\; por\;f(x)=sen(x-\frac{pi}{4})[/latex]
Consegui descobrir o período e a imagem, mas na hora de construir o gráfico e substituir os pontos, não bate com a resolução
Minha tentativa de construção do gráfico ficou assim:
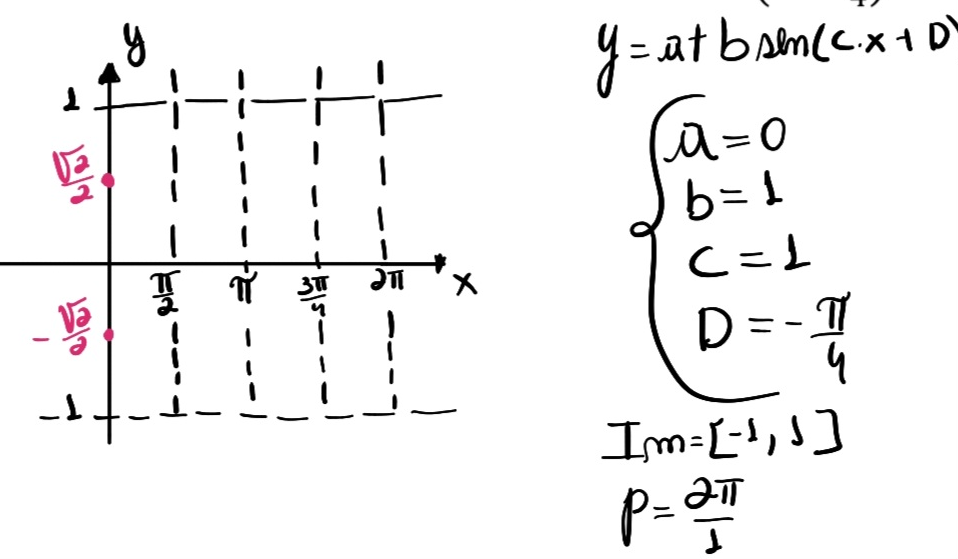
Ai eu tentei substituir os pontos f(0) e f(pi/2) p construir o gráfico, e não bateu com o gráfico da resolução, alguém pode me explicar o pq?
[latex]f:\mathbb{R}\rightarrow \mathbb{R} \; dada\; por\;f(x)=sen(x-\frac{pi}{4})[/latex]
Consegui descobrir o período e a imagem, mas na hora de construir o gráfico e substituir os pontos, não bate com a resolução
Minha tentativa de construção do gráfico ficou assim:
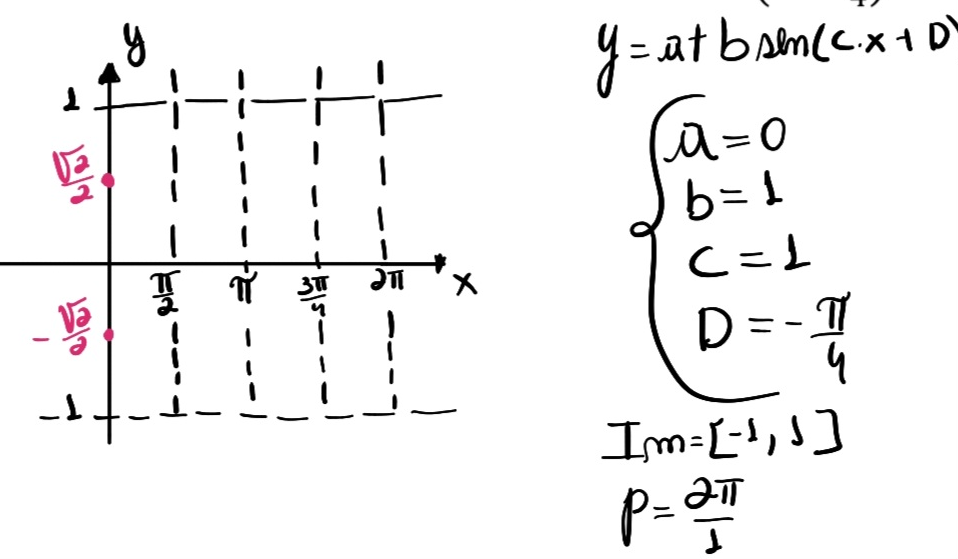
Ai eu tentei substituir os pontos f(0) e f(pi/2) p construir o gráfico, e não bateu com o gráfico da resolução, alguém pode me explicar o pq?

Lucas_Braz- Iniciante
- Mensagens : 36
Data de inscrição : 14/02/2023
Idade : 24
Localização : 082
Giovana Martins gosta desta mensagem
 Re: Construção de um gráfico de uma função do tipo seno
Re: Construção de um gráfico de uma função do tipo seno
Veja se você consegue entender: note que entre 7∏/4 e 3∏/4 há uma distância ∏ constante, pois a função é periódica. Assim, somando ou subtraindo ∏ a partir dos pontos de referência (3∏/4 e 7∏/4) você obtém todos os trechos da senoide.
[latex]\mathrm{Dado\ que\ -1\leq sin(\theta )\leq 1,para\ \theta =x-\frac{\pi }{4}\ \therefore\ -1\leq sin\left ( x-\frac{\pi }{4} \right )\leq 1\ \therefore\ Im(f)=[-1,1]}[/latex]
[latex]\mathrm{Sendo\ f(x)=a+bsin(cx-d)\ \therefore\ P=\frac{2\pi}{|c|}\to P=\frac{2\pi }{|1|}\ \therefore\ P=2\pi }[/latex]
[latex]\mathrm{Para\ x=0\ \therefore\ f(x)=sin\left ( -\frac{\pi }{4} \right )=-sin\left ( \frac{\pi }{4} \right )=-\frac{\sqrt{2}}{2}\ \therefore\ A\left ( 0,-\frac{\sqrt{2}}{2} \right )}[/latex]
[latex]\mathrm{Para\ f(x)=1\ \therefore\ sin\left ( x-\frac{\pi }{4} \right )=1=sin\left ( \frac{\pi }{2} \right )\ \therefore\ x=\frac{3\pi }{4}}[/latex]
[latex]\mathrm{Para\ f(x)=-1\ \therefore\ sin\left ( x-\frac{\pi }{4} \right )=-1=sin\left ( \frac{3\pi }{2} \right )\ \therefore\ x=\frac{7\pi }{4}}[/latex]

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Lucas_Braz gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» função do tipo seno
» Domínio da função e construção do gráfico
» Gráfico de função seno
» PUCsp gráfico da função seno
» Construção de gráfico
» Domínio da função e construção do gráfico
» Gráfico de função seno
» PUCsp gráfico da função seno
» Construção de gráfico
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












