Exprimir o volume do tetraedro em função de arestas
3 participantes
Página 1 de 1
 Exprimir o volume do tetraedro em função de arestas
Exprimir o volume do tetraedro em função de arestas
1. Num tetraedro (não necessariamente regular), duas arestas opostas têm o mesmo comprimento a e são perpendiculares entre si. Além disso, cada uma delas é perpendicular a uma linha de cumprimento b que liga os seus pontos médios. Exprimir o volume do tetraedro em função de a e b e demonstrar a resposta.
Na possibilidade representação gráfica.
Na possibilidade representação gráfica.
Última edição por Zeis em Seg 29 Jan 2024, 10:47, editado 1 vez(es)
Zeis- Mestre Jedi

- Mensagens : 530
Data de inscrição : 16/03/2020
 Re: Exprimir o volume do tetraedro em função de arestas
Re: Exprimir o volume do tetraedro em função de arestas
Por favor reveja o enunciado, acho que está truncado. Além disso está confuso.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Exprimir volume tetraedro
Exprimir volume tetraedro
Corrigido enunciado.
Zeis- Mestre Jedi

- Mensagens : 530
Data de inscrição : 16/03/2020
 Re: Exprimir o volume do tetraedro em função de arestas
Re: Exprimir o volume do tetraedro em função de arestas
Olá,
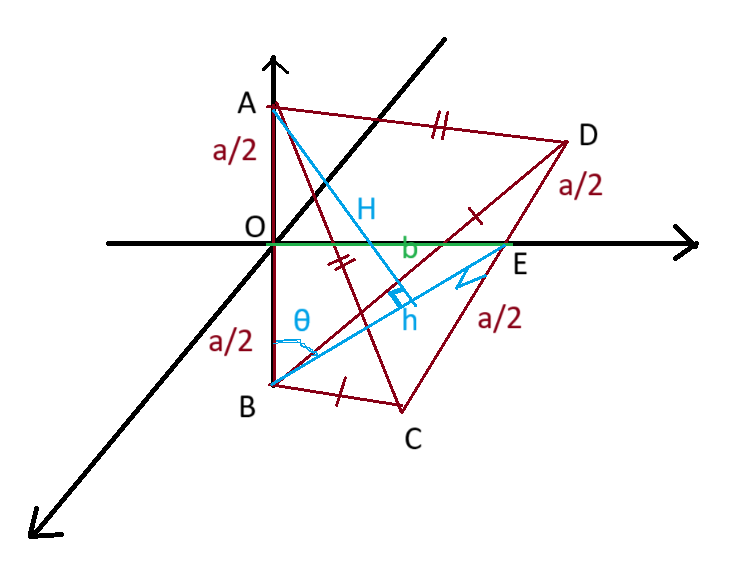
Acredito que o correto seria: "duas arestas opostas têm o mesmo comprimento a e são ortogonais entre si".
Nesse caso, temos:
(i) A área do ∆BCD é dada por:
[BCD] = ah/2 = (a/2)*√(b²+a²/4)
(ii) Note que do ∆BOE: tgθ = 2b/a ⇒ sinθ = b/√(b²+a²/4)
(iii) H = ABsinθ = ab/√(b²+a²/4)
Por fim, o volume é:
V = H[BCD]/3 = a²b/6.
Acredito que o correto seria: "duas arestas opostas têm o mesmo comprimento a e são ortogonais entre si".
Nesse caso, temos:
(i) A área do ∆BCD é dada por:
[BCD] = ah/2 = (a/2)*√(b²+a²/4)
(ii) Note que do ∆BOE: tgθ = 2b/a ⇒ sinθ = b/√(b²+a²/4)
(iii) H = ABsinθ = ab/√(b²+a²/4)
Por fim, o volume é:
V = H[BCD]/3 = a²b/6.

____________________________________________
Cha-la head-cha-la

Vitor Ahcor- Monitor

- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Medeiros gosta desta mensagem
 Re: Exprimir o volume do tetraedro em função de arestas
Re: Exprimir o volume do tetraedro em função de arestas
uma solução "malandra".
Seja o tetraedro inscrito num paralelepípedo de arestas {\(\ell,\, \ell,\, b \)}. Tal tetraedro é construído com as diagonais ortogonais das faces opostas do paralelepípedo, conforme a figura.
Note que, conf. enunciado, o tetraedro tem duas arestas de medida a que distam b uma da outra.
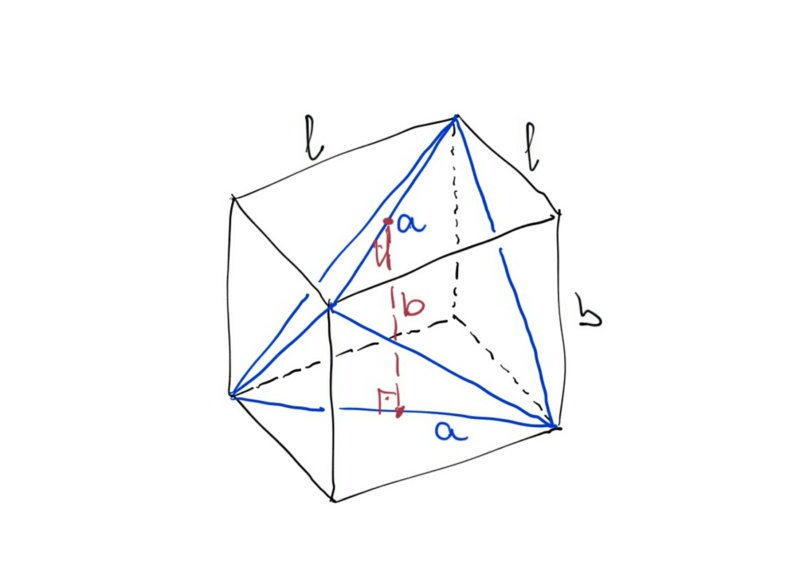
por construção --> \(a=\ell\sqrt{2}\,\,\rightarrow\,\,\ell=a \cdot \frac{\sqrt{2}}{2} \)
volume do paralelepípedo --> \( V_p = \ell . \ell . b = \frac{a².b}{2} \)
O volume do paralelepípedo é três vezes o volume do tetraedro nele inscrito, então
volume do tetraedro --> \(V_t = \frac{V_p}{3}\,\rightarrow\, \boxed{\,V_t = \frac{a².b}{6}\,} \)
___________________________________________________________________
Note que se b = \(\ell\), temos um cubo e o tetraedro é regular com volume --> \(V_t = \frac{a³\sqrt{2}}{12} \)
Seja o tetraedro inscrito num paralelepípedo de arestas {\(\ell,\, \ell,\, b \)}. Tal tetraedro é construído com as diagonais ortogonais das faces opostas do paralelepípedo, conforme a figura.
Note que, conf. enunciado, o tetraedro tem duas arestas de medida a que distam b uma da outra.

por construção --> \(a=\ell\sqrt{2}\,\,\rightarrow\,\,\ell=a \cdot \frac{\sqrt{2}}{2} \)
volume do paralelepípedo --> \( V_p = \ell . \ell . b = \frac{a².b}{2} \)
O volume do paralelepípedo é três vezes o volume do tetraedro nele inscrito, então
volume do tetraedro --> \(V_t = \frac{V_p}{3}\,\rightarrow\, \boxed{\,V_t = \frac{a².b}{6}\,} \)
___________________________________________________________________
Note que se b = \(\ell\), temos um cubo e o tetraedro é regular com volume --> \(V_t = \frac{a³\sqrt{2}}{12} \)

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Vitor Ahcor gosta desta mensagem
 Re: Exprimir o volume do tetraedro em função de arestas
Re: Exprimir o volume do tetraedro em função de arestas
Muito boa a solução Medeiros, a construção foi sagaz 
____________________________________________
Cha-la head-cha-la

Vitor Ahcor- Monitor

- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
 Re: Exprimir o volume do tetraedro em função de arestas
Re: Exprimir o volume do tetraedro em função de arestas
se eu achar um modo de trabalhar o mínimo possível, é o que eu faço.Vitor Ahcor escreveu:Muito boa a solução Medeiros, a construção foi sagaz :)

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» Volume do tetraedro
» tetraedro regular + arestas reversas
» Um tetraedro regular, cujas as arestas medem
» Exprimir a função
» Volume do Tetraedro
» tetraedro regular + arestas reversas
» Um tetraedro regular, cujas as arestas medem
» Exprimir a função
» Volume do Tetraedro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












