plano de Argand Gauss

por Rennan Santos Sáb 20 Jan 2024, 23:37

Considere no plano de Argand Gauss os números complexos z = x + yi, em que x e y são números reais e i²= -1, tais que |z+2+2i| ≤ 1. O módulo do complexo z de menor argumento que satisfaz a equação é

A) 2√2
B) 2
C)√7
D) 3

por **Giovana Martins** Dom 21 Jan 2024, 06:38

[latex]\\\mathrm{\ \ \ \ \ \ \ \ \ \ \ |z+2+2i|\leq 1\to |x+yi+2+2i|\leq 1\to |(x+2)+(y+2)i|\leq 1}\\\\ \mathrm{\ \ \ \ Dado\ que\ |z|=\sqrt{x^2+y^2}\ \therefore\ (x+2)^2+(y+2)^2\leq 1\ \therefore\ O(-2,-2)\ e\ R=1}\\\\ \mathrm{\ \ \ \ \ A\ reta\ que\ cont\acute{e}m\ os\ pontos\ A,B,C\ e\ O\ \acute{e}\ dada\ por:y=x.\ Deste\ modo:}\\\\ \mathrm{\ \ \ \left\{\begin{matrix} \mathrm{(x+2)^2+(y+2)^2= 1}\\ \mathrm{y=x} \end{matrix}\right.\ \therefore\ B\left ( \frac{1}{\sqrt{2}}-2,\frac{1}{\sqrt{2}}-2 \right )\ e\ C\left (- \frac{1}{\sqrt{2}}-2,-\frac{1}{\sqrt{2}}-2 \right )}\\\\ \mathrm{\ \ \ \ \ \ \ Da\ figura:AB=\frac{\left |\frac{1}{\sqrt{2}}-2 \right |}{cos(45^{\circ})}=2\sqrt{2}-1\ e\ AC=\frac{\left |- \frac{1}{\sqrt{2}}-2 \right |}{cos(45^{\circ})}=2\sqrt{2}+1}\\\\ \mathrm{Pelo\ Teorema\ das\ Cordas:|z|_{Arg,min}=\sqrt{AB\cdot AC}=\sqrt{(2\sqrt{2}-1)\cdot (2\sqrt{2}+1)}=\sqrt{7}}[/latex]

por Zeroberto Dom 21 Jan 2024, 16:47

Olá! Queria propor uma solução alternativa. Talvez ela não tenha ficado muito clara, então vou explicar o raciocínio:

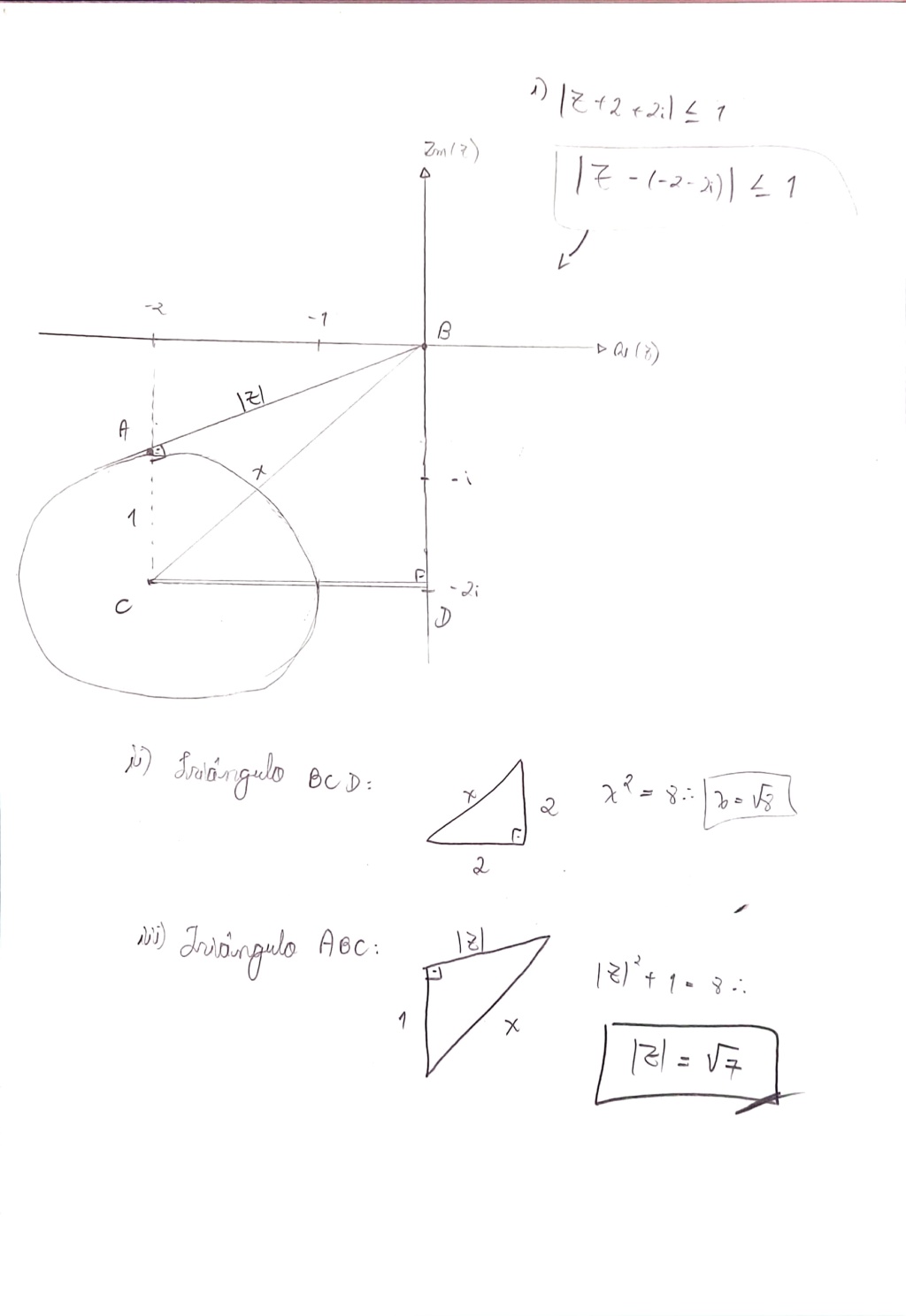
A primeira coisa que fiz foi "quebrar" o módulo inicial de tal maneira que ficasse da forma \( |Z_1 - Z_2| \), já que isso representa a distância entre esses dois complexos. Fazendo isso, ficamos com a equação que escrevi lá em cima. Ela significa que a distância entre um número complexo Z e o complexo (-2 - 2i) era menor ou igual a um. Isso é característica de uma circunferência.

Em seguida, desenhei essa circunferência (que mais parece uma geleia). Se o enunciado pede o complexo de menor argumento, então aquele que for o primeiro a tocar em algum ponto da circunferência é o número pedido, e esse complexo passa por uma reta tangente à circunferência. O resto foi pitágoras.

Lembro de uma questão do ITA com um raciocínio parecido. Se quiser eu posso te mandar o vídeo da resolução dela. O professor explica de uma maneira bem mais clara. Qualquer dúvida é só falar!

OBS: O desenho da Giovana mostra bem que o ponto A não coincide com a abcissa do centro dessa circunferência. Meu desenho que ficou ruim mesmo e pode levar a esse erro do ponto A.