Derivadas:Conceitos iniciais

por Dias_007 Seg 25 Dez 2023, 16:56

Considere a função f(x) = (x−1 )/(x+1) e seja f′(x) a sua derivada. Então, o valor de f′(2) é:
(A) 0 (B) 1/9 (C) 2/9 (D) 1/3 (E) 4/9
Estou sem o gabarito,alguém pode me explicar?

por **Giovana Martins** Seg 25 Dez 2023, 17:09

Não deu para entender o enunciado.

por Dias_007 Seg 25 Dez 2023, 17:13

editei o enunciado...

por **Giovana Martins** Seg 25 Dez 2023, 17:19

[latex]\\\mathrm{\ \ \ \ Regra\ do\ quociente:\left [ \frac{u(x)}{v(x)} \right ]'=\frac{v(x)u'(x)-u(x)v'(x)}{[v(x)]^2}}\\\\ \mathrm{\ \ \ \ \ \ \ \frac{d}{dx}\left ( \frac{x-1}{x+1} \right )=\frac{(x+1)\frac{d}{dx}(x-1)-(x-1)\frac{d}{dx}(x+1)}{(x+1)^2}}\\\\ \mathrm{\ \ \ \ \ \ \ \frac{d}{dx}\left ( \frac{x-1}{x+1} \right )=\frac{(x+1)\cdot1-(x-1)\cdot 1}{(x+1)^2}=\frac{2}{(x+1)^2}}\\\\ \mathrm{\therefore\ \left [ \frac{d}{dx}\left ( \frac{x-1}{x+1} \right ) \right ]_{x=2}=\frac{2}{(2+1)^2}\ \therefore\ \left [ \frac{d}{dx}\left ( \frac{x-1}{x+1} \right ) \right ]_{x=2}=\frac{2}{9}}[/latex]

por **Giovana Martins** Seg 25 Dez 2023, 17:20

Dias_007 escreveu:
editei o enunciado...

Obrigada.

por castelo_hsi Seg 25 Dez 2023, 17:31

Revisando a propriedade e aplicando:

$Derivadas:Conceitos iniciais Png.latex?f%28x%29%3D%5Cfrac%7Bg%28x%29%7D%7Bh%28x%29%7D%5Crightarrow%20f%27%28x%29%3D%5Cfrac%7Bg%27%28x%29.h%28x%29-g%28x%29.h%27%28x%29%7D%7B%5Bh%28x%29%5D%5E%7B2%7D%7D%20%5C%5C%5C%5C%20f%27%28x%29%3D%5Cfrac%7B1x%5E%7B0%7D.%28x+1%29-%28x-1%29$

Por fim:

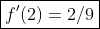
$Derivadas:Conceitos iniciais 9%7D$