07 pontos médios e áreas
3 participantes
Página 1 de 1
07 pontos médios e áreas
por Analise Sousa Pereira Seg 04 Dez 2023, 11:37
um paralelogramo ABCD, onde M é o ponto médio de CD. P é o ponto de interseção do segmento AM com a diagonal BD. a área do triângulo DPM é igual a 1 cm2. a área do paralelogramo ABCD, em cm2, é igual a:
Gabarito 12
Adaptado de ibam 2023
Gabarito 12
Adaptado de ibam 2023
Última edição por Analise Sousa Pereira em Seg 04 Dez 2023, 14:03, editado 1 vez(es)
Analise Sousa Pereira- Recebeu o sabre de luz
- Mensagens : 189
Data de inscrição : 18/11/2023
Re: 07 pontos médios e áreas
por Elcioschin Seg 04 Dez 2023, 13:00
Tens o gabarito?
Um modo trabalhoso, usando GA:
Um modo trabalhoso, usando GA:
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Analise Sousa Pereira gosta desta mensagem
Re: 07 pontos médios e áreas
por Medeiros Ter 05 Dez 2023, 02:34
por G. Plana
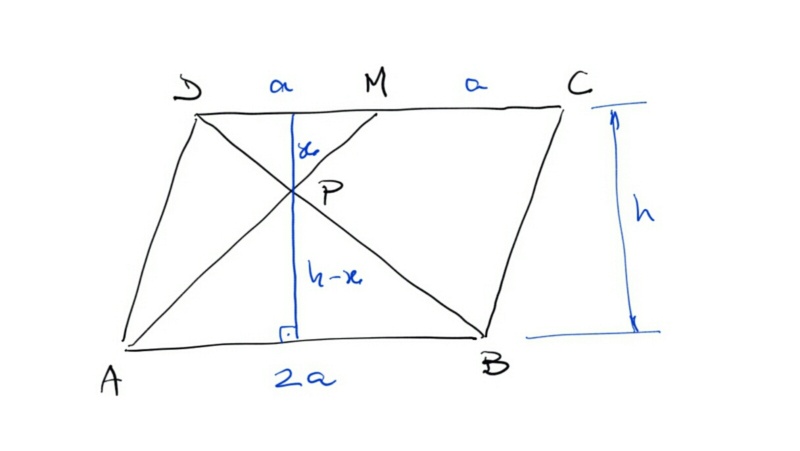
\( [DMP] = \frac{a.x}{2} = 1\ cm² \to\ ax = 2 \,\,\,\,\,\,\,\,\,(1) \)
\( \triangle ABP \sim \triangle DMP\ \to\ \frac{[ABP]}{[DMP]}=\left (\frac{2a}{a} \right )^{2}\ \to\
[ABP]=1.2^{2}=4\ cm² \)
\([ABP]=\frac{2a(h-x)}{2}=4\ \to\ a(h-x)=4\ \to\ ah-ax=4 \,\,\,\,\,\,\,\,\,(2) \)
\( (1)\ em\ (2):\ ah-2=4\ \to\ ah=6\ \to\ h=\frac{6}{a} \)
\( [ABCD]=2a.h = 2a\cdot\frac{6}{a}\ \to\ \boxed{\,[ABCD]=12\ cm²\,} \)
\( [DMP] = \frac{a.x}{2} = 1\ cm² \to\ ax = 2 \,\,\,\,\,\,\,\,\,(1) \)
\( \triangle ABP \sim \triangle DMP\ \to\ \frac{[ABP]}{[DMP]}=\left (\frac{2a}{a} \right )^{2}\ \to\
[ABP]=1.2^{2}=4\ cm² \)
\([ABP]=\frac{2a(h-x)}{2}=4\ \to\ a(h-x)=4\ \to\ ah-ax=4 \,\,\,\,\,\,\,\,\,(2) \)
\( (1)\ em\ (2):\ ah-2=4\ \to\ ah=6\ \to\ h=\frac{6}{a} \)
\( [ABCD]=2a.h = 2a\cdot\frac{6}{a}\ \to\ \boxed{\,[ABCD]=12\ cm²\,} \)
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Analise Sousa Pereira gosta desta mensagem
Tópicos semelhantes» Semicircunferências - (pontos médios)
» M e N são os pontos médios respectivos dos la
» pontos medios
» Os Pontos Médios
» trapézios pontos médios
» M e N são os pontos médios respectivos dos la
» pontos medios
» Os Pontos Médios
» trapézios pontos médios
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
