Cubo inscrito em um cone - dúvida na resolução

por Zeroberto Sex 17 Nov 2023, 22:20

Um cubo de aresta a é inscrito em um cone equilátero. Calcule a geratriz do cone.

Cubo inscrito em um cone - dúvida na resolução Aref_c11

Gabarito: \( g = \frac{a(2+\sqrt6)}{3} \)

Boa noite, pessoal! Poderiam me dar uma ajuda para entender onde estou errando? Fiz uma figura para ajudar na visualização do meu raciocínio:

Cubo inscrito em um cone - dúvida na resolução Aref_c12

Minha ideia foi trabalhar com semelhança. Como o cone é reto, puxei uma altura para coincidir bem no centro do cone e do cubo. A altura, juntamente com o raio da base e a geratriz formariam um grande triângulo retângulo, assim como aquela parte acima do cubo também. A partir disso, tentei fazer a semelhança, mas não bateu com o gabarito:

[latex]\frac{ \frac{g\sqrt3}{2}}{ \frac{g\sqrt3}{2} - a} = \frac{ \frac{g}{2} } {\frac{a\sqrt2}{2} } \implies [/latex]

[latex] \frac{ \frac{g\sqrt3}{2} } { \frac{g\sqrt3 - 2a}{2} } = \frac{2g}{2a\sqrt2} \implies \frac{g\sqrt3}{g\sqrt3 - 2a} = \frac{g}{a\sqrt2} \implies [/latex]

[latex]a\sqrt6 = g\sqrt3 - 2a \implies a(2+\sqrt6) = g\sqrt3 \therefore \boxed{g = \frac{a\sqrt3}{3}(2+\sqrt6)}[/latex]

por **Medeiros** Sex 17 Nov 2023, 22:43

Erro nenhum, Zeroberto. Acho que o gabarito esqueceu aquela raiz de 3.
Concordo com sua resolução.

por Zeroberto Sex 17 Nov 2023, 22:52

Medeiros escreveu:Erro nenhum, Zeroberto. Acho que o gabarito esqueceu aquela raiz de 3.
Concordo com sua resolução.

Ufa! Já estava entrando em parafuso achando que tinha errado alguma continha boba. Obrigado Medeiros!

Aliás, eu percebi que a imagem do triângulo ficou gigantesca quando eu postei. Você sabe como reduzir o tamanho? Ou pelo menos como reduzi-la quando eu adicioná-la ao post?

por **Giovana Martins** Sex 17 Nov 2023, 23:15

por **Giovana Martins** Sex 17 Nov 2023, 23:17

Postei, porque eu já havia esboçado a questão aqui.

Não utilizei a propriedade 1. Apenas a enunciei.

por **Giovana Martins** Sex 17 Nov 2023, 23:22

Nota: na propriedade 2, onde está escrito "meriana" leia-se "meridiana".

por **Giovana Martins** Sex 17 Nov 2023, 23:28

Zeroberto escreveu:
Medeiros escreveu:
Erro nenhum, Zeroberto. Acho que o gabarito esqueceu aquela raiz de 3.
Concordo com sua resolução.
Ufa! Já estava entrando em parafuso achando que tinha errado alguma continha boba. Obrigado Medeiros!

Aliás, eu percebi que a imagem do triângulo ficou gigantesca quando eu postei. Você sabe como reduzir o tamanho? Ou pelo menos como reduzi-la quando eu adicioná-la ao post?

Curioso você ter conseguido postar uma imagem deste tamanho. Para eu conseguir postar uma imagem aqui no fórum é uma luta.

Toda vez aparece a mensagem: "post is too long" (acho que é isso) por causa do tamanho da imagem que com certeza é menor do que a que você postou (pelo menos aparenta kkk).

Não sei como você fez isso.

por Zeroberto Sáb 18 Nov 2023, 07:14

Giovana Martins escreveu:
Curioso você ter conseguido postar uma imagem deste tamanho. Para eu conseguir postar uma imagem aqui no fórum é uma luta.

Toda vez aparece a mensagem: "post is too long" (acho que é isso) por causa do tamanho da imagem que com certeza é menor do que a que você postou (pelo menos aparenta kkk).

Não sei como você fez isso.

Pior que postei normalmente como eu sempre posto, acho que não fiz nada demais. Depois eu tiro um print, pelo computador, da tela na qual eu anexo as fotos, estou pelo celular agora e não sei bem como mexer no fórum por aqui.

Aliás, que solução bacana para o problema, Giovana.

por Zeroberto Sáb 18 Nov 2023, 12:20

Voltando aos prints que tinha comentado. Eu faço essa sequência aqui:

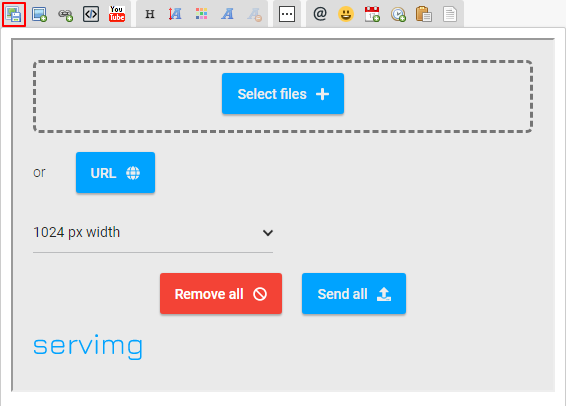
Cubo inscrito em um cone - dúvida na resolução Respon10

Cubo inscrito em um cone - dúvida na resolução Respon11

Clicava naquele ícone lá no canto superior esquerdo, ia no "send all", e quando aparecia essa segunda tela, ia no "insert all". Sempre achei "estranho" esse jeito de postar, e como ainda não testei todas as funcionalidades daquela barra lá em cima, nunca soube se era a melhor forma de enviar uma imagem kkkkkk

Por funcionar na primeira vez que tentei, acabei ficando com esse jeito de inserir as imagens. Nunca soube se era o jeito certo, mas se funcionou, está ótimo. Até hoje não me limitou quanto ao tamanho da foto. Apesar que eu sempre tiro prints, então a imagem fica relativamente leve, ainda que seja extensa em tamanho. Será que não seria isso?