Perímetro da seção de um cubo - Aref

por Zeroberto Seg 23 Out 2023, 19:16

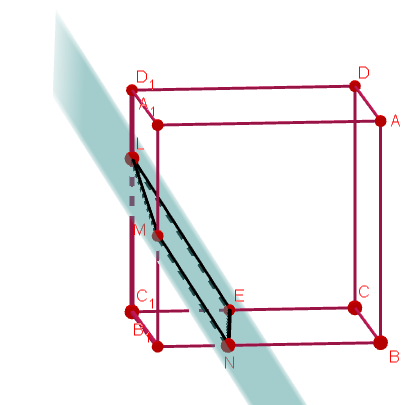
É dado um cubo \(ABCD A_1 B_1 C_1 D_1\), com aresta a. Sobre a resta \(C_1 D_1\) toma-se um ponto L, com \( C_1 L = \frac{3a}{4} \); sobre a aresta \(A_1 B_1\) toma-se o ponto M, com \( A_1 M = \frac{a}{2} \); sobre a aresta \( BB_1\), toma-se o ponto N, com \(B_1 N = \frac{a}{4} \). Calcule o perímetro da seção determinada no cubo, por um plano conduzido pelos pontos L, M e N.

\(Gabarito: 2p = \frac{a}{8} (2\sqrt17 + 5\sqrt5 + \sqrt65) \)

por **Giovana Martins** Seg 20 Nov 2023, 15:28

por **Giovana Martins** Seg 20 Nov 2023, 15:31

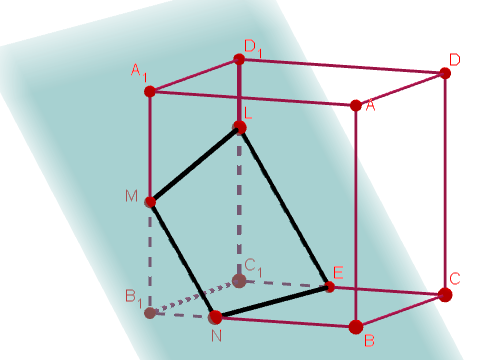
Inicialmente, vou deixar uma imagem do problema para quem queira tentar algo (sendo bem sincera, estou com uma preguicinha para tentar resolver problema ...).

Se ninguém mexer no problema, em algum momento eu tento postar algo.

A princípio, descobrir o comprimento do segmento NE vai ser um pouquinho chato.

por **Medeiros** Seg 20 Nov 2023, 16:31

Giovana,
estou com este problema atravessado desde que ele foi postado.

Não tenho tido muito tempo contínuo para dedicar e o tenho deixado meio de lado. Minha dificuldade, aliás a única da questão, é obter a posição exata do ponto E (seu desenho). Você o jogou no meio da aresta, parece um bom palpite mas fico imaginando que talvez possa ser numa divisão de 3/4 ou 3/8, não sei, ainda não fiz qualquer cálculo a esse respeito.

Só o que fiz até agora são alguns esboços para encontrar o melhor desenho -- a partir de um bom desenho posso começar a trabalhar. O seu desenho é diferente de todos os meus esboços e me parece o melhor até agora.

Aguardo sua resolução.

por **Giovana Martins** Seg 20 Nov 2023, 16:37

Medeiros escreveu:
Giovana,
estou com este problema atravessado desde que ele foi postado.

Não tenho tido muito tempo contínuo para dedicar e o tenho deixado meio de lado. Minha dificuldade, aliás a única da questão, é obter a posição exata do ponto E (seu desenho). Você o jogou no meio da aresta, parece um bom palpite mas fico imaginando que talvez possa ser numa divisão de 3/4 ou 3/8, não sei, ainda não fiz qualquer cálculo a esse respeito.

Só o que fiz até agora são alguns esboços para encontrar o melhor desenho -- a partir de um bom desenho posso começar a trabalhar. O seu desenho é diferente de todos os meus esboços e me parece o melhor até agora.

Aguardo sua resolução.

Então, eu também já peguei para fazer esta questão em algum outro momento, mas fiquei com preguiça de tentar achar esse comprimento, mas no pouco que vi, me parece que vai dar um pouquinho de trabalho, daí como tem que fazer algumas construções não consegui mexer tanto assim.

A propósito, não foi minha intenção supor que o ponto E está na metade do segmento. Foi meio sem querer já que eu fiz o desenho sem usar escala. Só fui colocando os pontos no Geogebra e construindo.

Ainda não tenho uma resolução, mas vou tentar propor algo. Se eu conseguir eu posto.

por **petras** Seg 20 Nov 2023, 17:16

Giovana Martins escreveu:

Aproveitando o desenho da Giovana teremos

[latex]\triangle MNB1:MN^2=(\frac{a}{4})^2+(\frac{a}{2})^2 \implies \boxed{MN = \frac{a\sqrt5}{4}}\\ MO \perp D_1C_1 (O \in D_1C_1)\implies \triangle MLO: LM^2 = a^2+(\frac{a}{4})^2 \implies \boxed{LM=\frac{a\sqrt{17}}{4}}\\ \triangle MB_1N \sim \triangle LC_1E :\\ C1E.\frac{a}{2}=\frac{a}{4}.\frac{3a}{4} \therefore C_1E = \frac{3a}{8}\\ \triangle LC_1E: LE^2 = (\frac{3a}{4})^2+(\frac{3a}{8})^2 \therefore \boxed{LE =\frac{3a\sqrt5}{8} }\\ P \perp C_1E:(P \in C_1E) \implies \triangle NPE: NE^2 = a^2+(\frac{3a}{8}-\frac{a}{4})^2 \therefore \boxed{NE=\frac{a\sqrt65}{8}}\\ 2p =\frac{a\sqrt5}{4} +\frac{3a\sqrt5}{8}+\frac{a\sqrt{17}}{4}+\frac{a\sqrt{65}}{8}=\\ \frac{5a\sqrt5}{8}+\frac{a\sqrt{17}}{4}+\frac{a\sqrt{65}}{8}=\boxed{\frac{a}{8}(5\sqrt5+2\sqrt{17}+\sqrt{65})} [/latex]

por **Medeiros** Seg 20 Nov 2023, 19:01

Pretas,
não imagino com base em quê você concluiu que o triângulo LC1E é semelhante ao MB1B; acho que foi um ato de coragem.

Em todo o caso, é verdade pois resolvi usando geometria analítica (ferramenta que evito usar) e realmente C1E = (3/ Cool

.a.

por **Giovana Martins** Seg 20 Nov 2023, 20:31

Eu também não consegui pegar a ideia de como os triângulos são semelhantes.

por **petras** Ter 21 Nov 2023, 00:36

Medeiros escreveu:Pretas,
não imagino com base em quê você concluiu que o triângulo LC1E é semelhante ao MB1B; acho que foi um ato de coragem.

Em todo o caso, é verdade pois resolvi usando geometria analítica (ferramenta que evito usar) e realmente C1E = (3/.a.

Pode ter sido coragem demais...rsss

Vou pensar com mais cuidado o porque da retas serem paralelas ...

por **Medeiros** Ter 21 Nov 2023, 00:46

petras escreveu:Pode ter sido coragem demais...rsss

Mas sendo MN || LE e B1N || C1E não teríamos o ângulo MNB1 congruente com LEC1?

Grato pela atenção da resposta, Petras.

Mas aí é que está o ponto que me enrosca: como podemos garantir que LE // MN se não sabemos ainda onde está o ponto E? Pois é justamente a posição do ponto E que desejamos descobrir, depois fica fácil.