O pentágono e a hipotenusa

Ao longo dos lados de um pentágono regular de lado a traçam-se seis triângulos retângulos congruentes. Calcular o valor da hipotenusa ℓ
desses triângulos retângulos.

Gabarito: a(1+√5)


Bom dia, senhores(a). Poderiam me dar uma força nessa questão, por gentileza? Desde já, agradeço!!

Faltou BM = L na figura:

Elcioschin escreveu:Faltou BM = L na figura:

Opa, grande mestre. O senhor poderia mostrar como você fez para relacionar a hipotenusa "L" com o lado "a" do pentágono, por gentileza?

Carlos Heitor (EPCAr) escreveu:

Elcioschin escreveu:Faltou BM = L na figura:

Opa, grande mestre. O senhor poderia mostrar como você fez para relacionar a hipotenusa "L" com o lado "a" do pentágono, por gentileza?

Boa noite, pessoal. Alguém poderia me ajudar a concluir a solução do mestre, por gentileza?

Carlos Heitor (EPCAr) escreveu:

Carlos Heitor (EPCAr) escreveu:

Elcioschin escreveu:Faltou BM = L na figura:

Opa, grande mestre. O senhor poderia mostrar como você fez para relacionar a hipotenusa "L" com o lado "a" do pentágono, por gentileza?

Boa noite, pessoal. Alguém poderia me ajudar a concluir a solução do mestre, por gentileza?

O triÂngulo (36-54-90) é um triângulo notável onde os lados correspondem a [latex]a(\sqrt{10-2\sqrt5}):a(\sqrt5+1):4a[/latex]


https://www.youtube.com/watch?v=icl7Sxf5nFE

petras escreveu:

Carlos Heitor (EPCAr) escreveu:

Carlos Heitor (EPCAr) escreveu:

Elcioschin escreveu:Faltou BM = L na figura:

Opa, grande mestre. O senhor poderia mostrar como você fez para relacionar a hipotenusa "L" com o lado "a" do pentágono, por gentileza?

Boa noite, pessoal. Alguém poderia me ajudar a concluir a solução do mestre, por gentileza?

O triÂngulo (36-54-90) é um triângulo notável onde os lados correspondem a [latex]a(\sqrt{10-2\sqrt5}):a(\sqrt5+1):4a[/latex]


https://www.youtube.com/watch?v=icl7Sxf5nFE

Bom dia, mestre. Pô, agradeço pela resposta, eu desconhecia esse tirângulo notável.

O senhor poderia me mostrar como você fez depois para relacionar o lado do pentágono? Agradeço!

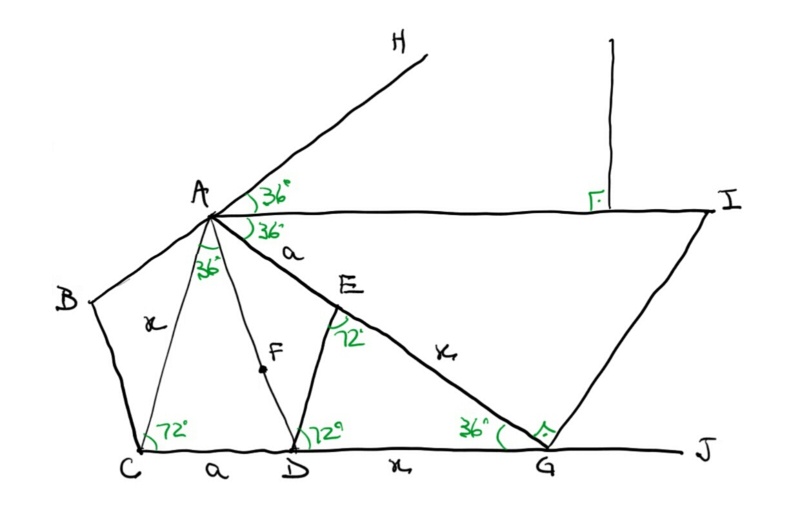
Carlos Heitor,
não sei se ainda lhe interessa mas segue um forma de relacionar o lado do pentágono (a) com aquela hipotenusa (ℓ). De qualquer forma, fica para consulta de algum colega que possa posteriormente se interessar.



SOBRE O PENTÁGONO REGULAR

[latex]\\\mathrm{\hat{a}ngulo\ interno} \to \alpha_i=\frac{n-2}{n}\cdot 180^{\circ} \to \mathrm{pent\acute{a}gono\ n=5} \to \boxed{\alpha_i=108^{\circ}}[/latex]

∆ABC é isósceles (pernas = a, enunciado), então ângulo AˆCB = CÂB = 36º.
Todas as diagonais têm mesma medida.
Quanto mede a diagonal do pentágono?
AC = AD  --->  ∆ABC ≡ ∆AED (LLL), logo ângulo DÂE = CÂB = 36º.
.:. CÂD = 108º - 2*36º  --->  CÂD = 36º
∆ACD = isósceles  --->  AĈD = DÂC = 72º.


Seja CF = bissetriz de AĈD (por construção).
.:.  AĈF = DĈF = 72º/2 = 36º  ==>  CˆFD = CˆDF = 72º
.:.  ∆ACD, ∆CDF e ∆AFC são isósceles  ( obs:  ∆AFC ≡ ∆ABC )
==> CD = CF = AF = a
seja AC = x  --->  DF = x - a
[latex]\\\Delta CDF\sim \Delta ACD\ (AA)\ \to\ \frac{CD}{AC}=\frac{DF}{CD}\ \to\ \frac{a}{x}=\frac{x-a}{a}\\\\ x^{2}-ax-a^{2}=0\\ \Delta = a^{2}+4a^{2}=5a^{2}\\ x=\frac{a\pm a\sqrt{5}}{2}\ ,\ x>0\ \to\ \boxed{\ x=a\frac{\sqrt{5}+1}{2}\ }[/latex]


INÍCIO DA RESOLUÇÃO


GˆDE = GÊD = 72º -- âng. externo ao pentágono
.:.  DĜE = 36º
.:.  ∆GDE ≡  ∆ACD  (ALA)  ==>  GD = GE = x

HÂG = 72º (âng. externo pent.) e os 6 triângulos retângulos são congruentes (enunciado)  --->  AI = bissetriz de HÂG
.:.  HÂI = IÂG = 36º  (i)
AĜJ = 144º (âng. ext. ∆GDE)  (ii)
De (i) e (ii), IÂG + AĜJ = 36º + 144º = 180º  --->  pelo 5º postulado de Euclides, AI // CJ

Seja a mediana AM (h) e a altura GK do ∆AGI (h, também), ambas perpendiculares a CJ, evidentemente.


CD = a  --->  CM = MD = a/2  --->  MG = x + a/2

[latex]\\AI//CJ\ ,\ AM\perp{CJ}\ e\ GK\perp{AI}\ \therefore\ AM//CK[/latex]
[latex]\\\therefore\ AK=MG=x+\frac{a}{2}[/latex]
e lembrando que GA = x + a

[latex]\\\Delta AKG\sim \Delta AGI\ (AA)\ \to\ \frac{AK}{AG}=\frac{AG}{AI}\ \to\ \frac{x+\frac{a}{2}}{x+a}=\frac{x+a}{\ell}\\\\ \therefore\ \ell=\frac{(x+a)^{2}}{x+\frac{a}{2}}\\\\\\ \left\{\begin{matrix} x+a=a\frac{\sqrt{5}+1}{2}+a\frac{2}{2}=a\frac{\sqrt{5}+3}{2}\\\\ x+\frac{a}{2}=a\frac{\sqrt{5}+2}{2} \end{matrix}\right.\\\\\\ \ell=\frac{a^{2}\frac{14+6\sqrt{5}}{4}}{a\frac{\sqrt{5}+2}{2}}\ =\ a\frac{7+3\sqrt{5}}{\sqrt{5}+2}\ =\ a\frac{(7+3\sqrt{5})(\sqrt{5}-2)}{5-4}\\\\\\ \ell =a\left[7\sqrt{5}-14+15-6\sqrt{5} \right ]\ \to\ \color{Red}{\boxed{\ \ell=a(\sqrt{5}+1)\ }\ }[/latex]